
داستان باورنکردنی عدد پی؛ مهمترین و مرموزترین عدد جهان
دوشنبه 26 آبان 1404 - 12:00مطالعه 21 دقیقهآیا تابهحال عدد دیگری وجود داشته که تا این حد کنجکاوی بشر را برانگیخته کند؟ عددی که برایش جشن میگیرند، موضوع کتابها و آثار هنری میشود و زمانی، مایهی عذاب ریاضیدانان باستان بوده است؟ آیا عددی را میشناسید که به قدرت، شگفتی و شهرت جهانی «پی» (π) نزدیک شود؟
«پی» عددی است که آن را با ...۳٫۱۴۱۵۹ میشناسیم و ارقام اعشار آن تا ابد ادامه دارد. اما «پی» واقعاً چیست؟ چرا اینقدر خاص و مشهور است؟ چرا بینهایت رقم دارد و ما اصلاً چگونه از این واقعیت باخبر شدیم؟ آیا درست است که «پی» هر توالی عددی قابلتصوری را در خود جای داده است؟ ما چگونه توانستهایم این همه از ارقام آن را با دقت محاسبه کنیم و اصلاً چرا به خودمان این همه زحمت دادهایم؟
این داستان، سفری به درازای ۴۰۰۰ سال برای کشف راز یک عدد ساده و در عین حال، عمیقاً پیچیده است.

عددی پی چیست؟
عدد پی که نماد آن شانزدهمین حرف یونانی، π است و در انگلیسی بهصورت پای (Pi) تلفظ میشود، در دنیای محاسبات هندسی، نسبت محیط هر دایره به قطر آن است.
π = قطر/محیط دایره
نکتهی جالب اینکه مهم نیست اندازهی دایره چقدر باشد؛ چراکه این نسبت همیشه ثابت و برابر با عدد پی خواهد بود.

با عدد پی احتمالا به شکل اعشاری ۳٫۱۴ آشنا هستید؛ اما این رقم تقریبی است؛ چون پی، عدد «گنگ» است. این یعنی ارقام اعشاری آن نه بهپایان میرسد (مثل ۱٫۴ که میشود ۰٫۲۵) و نه تکراری است (مثل ۱٫۶ که میشود …۰٫۱۶۶۶۶۶). عدد پی تا ۱۸ رقم اعشار برابر است با: ۳٫۱۴۱۵۹۲۶۵۳۵۸۹۷۹۳۲۳۸. همانطورکه میبینید، در این زنجیره ۱۸ تایی، هیچ رقمی پشتسرهم تکرار نشده است و هیچ الگوی ثابتی در آن دیده نمیشود.
ازاینرو، لازم بود برای نشاندادن نسبت محیط به قطر مقدار مختصر و تقریبی نظیر ۳٫۱۴ یا نزدیکترین شکل کسری آن یعنی ۲۲/۷ در نظر گرفته شود. سال ۱۷۰۶، ویلیام جونز اولینبار حرف یونانی π را از کلمهی «محیط» در زبان یونانی (περιφέρεια) بهعنوان نماد عدد پی گرفت؛ اما حدود سی سال طول کشید تا بهعنوان ثابت استانداردی در ریاضی استفاده شود.

برای درک بهتر عدد پی، بیایید آزمایش ساده انجام دهیم. روی کاغذ با پرگار دایرهای بکشید و تکهای نخ بردارید و آن را یک بار دورتادور دایره قرار دهید. حالا نخ را صاف کنید. محیط دایره برابر با طول نخ است. آن را با خطکش اندازه بگیرید و عدد آن را یادداشت کنید. بعد با قراردادن خطکش از هر نقطهای از دایره تا نقطه دیگر بهطوریکه مرکز آن را قطع کند، قطر دایره را اندازه بگیرید. حالا اگر محیط دایره را بر قطر تقسیم کنید، تقریبا عدد ۳٫۱۴ بهدست میآید.
این آزمایش را با دایرههایی با اندازههای مختلف تکرار کنید. هر بار خواهید دید از تقسیم محیط دایره بر قطر همواره عدد تقریبی ۳٫۱۴ بهدست خواهد داد. بهعبارتدیگر، اگر چند تکه نخ برابر با طول قطر دایره داشته باشید، برای پوشاندن دور دایره به کمی بیشتر از سه تکه نخ نیاز خواهید داشت. این عدد پی است؛ نسبت ثابت محیط دایره بر قطر که ارقام اعشار آن تا بینهایت ادامه دارد و هیچگاه دو عدد تکراری پشتسرهم قرار نمیگیرند.
روشهای محاسبه عدد پی
محاسبه عدد پی از بعضی جهات بسیار ساده است؛ تنها کافی است محیط هر دایره را به قطر آن تقسیم کنید تا به عدد پی برسید.
اما از آنجایی که عدد پی (π) کاربردهای مهم بسیاری دارد، لازم است محاسبه آن را حداقل تا چند رقم اعشار یاد بگیریم. به هر حال، عدد پی ماشینحسابها از آسمان نازل نشده و کسی بوده که باید ابتدا آن را بهطور دستی و تقریبی محاسبه میکرده است. اما ریاضیدانان طول تاریخ برای محاسبه پی از چه روشهای استفاده میکردند؟ در ادامه با بعضی از این روشها آشنا خواهید شد.
اندازهگیری دایرهها برای محاسبه عدد پی (π)
اولین و واضحترین روش محاسبه پی (π) این است که کاملترین دایره ممکن را انتخاب کنید و بعد با اندازهگیری محیط و قطر آن، میزان پی را به دست آورید. این دقیقا همان کاری است که تمدنهای باستان انجام میدادند و این چنین بود که برای اولین بار فهمیدند در هر دایرهای، نسبت ثابتی پنهان است. اما مشکل این روش محاسبه، دقت بسیار پایین آن است. آیا میتوانید به اندازهگیری خطکش خود برای محاسبه ۱۰ رقم اعشار پی اعتماد کنید؟
استفاده از چند ضلعیها برای محاسبه عدد پی (π)
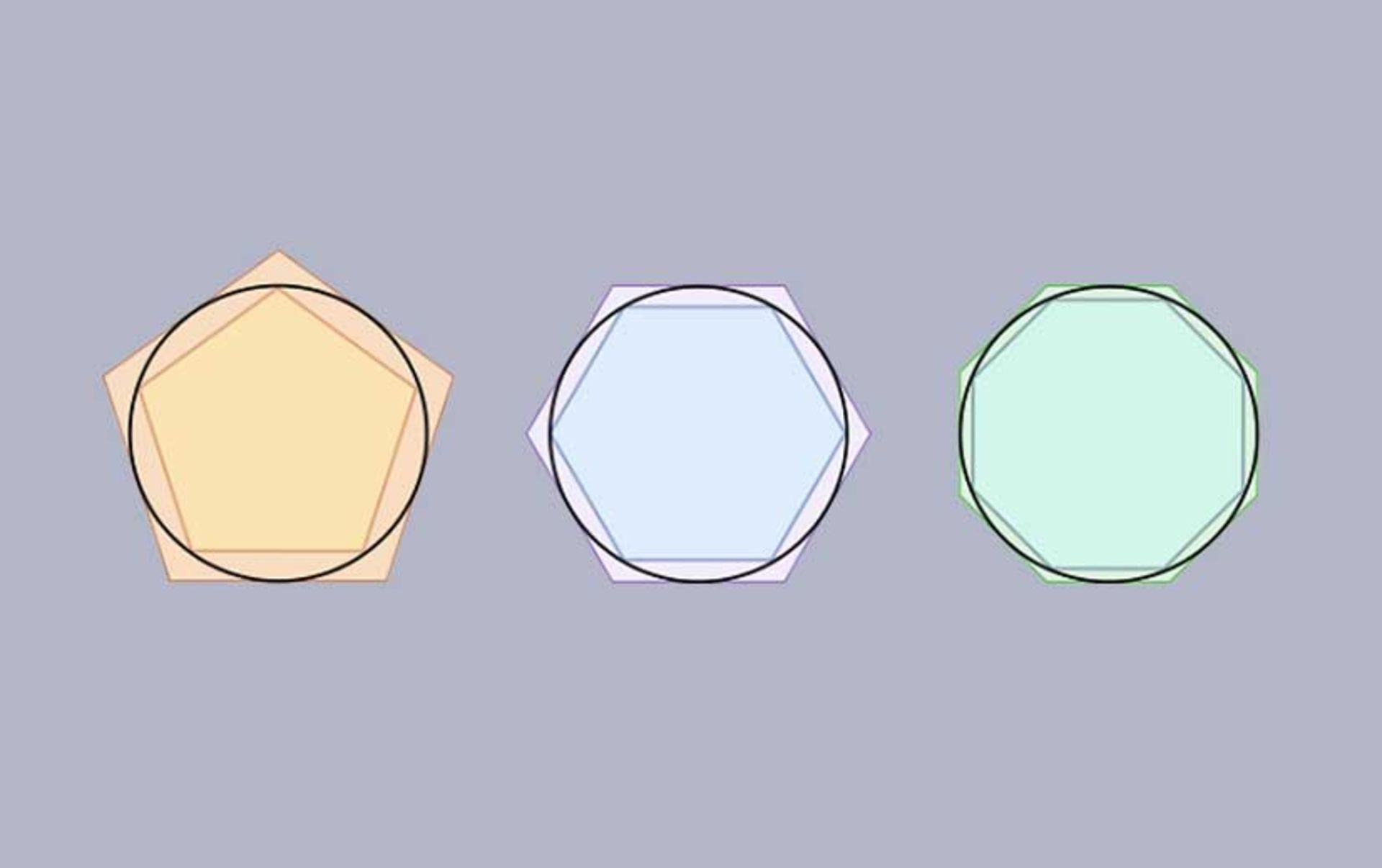
ارشمیدس، ریاضیدان یونان باستان، برای محاسبه تقریبی عدد پی روش جالبی ابداع کرد. او درون یک دایره، یک شش ضلعی منتظم کشید و بعد یک شش ضلعی منتظم دیگر را دورتادور و خارج از آن رسم کرد. ارشمیدس از این طریق توانست محیطها و قطرهای دو شش ضلعی را بهطور دقیق محاسبه کند و با تقسیم محیط بر قطر، میزان تقریبی عدد پی (π) را بدست آورد.
آیا عدد دیگری را میشناسید که به قدرت، شگفتی و شهرت جهانی عدد پی نزدیک شود
ارشمیدس بعدها راهی یافت تا تعداد اضلاع شش ضلعی خود را دو برابر کند و با نزدیکتر کردن شکل شش ضلعی به دایره، مقدار تقریبی دقیقتری از پی را محاسبه کرد. او این روش را چهار بار انجام داد تا اینکه به چند ضلعی با ۹۶ گوشه رسید. حالا عدد پی به دست آمده بین ۲۲۱/۷۱ و ۲۲/۷ بود. عدد کسری ۲۲/۷ از آن زمان تاکنون به عنوان یکی از محبوبترین و پرکاربردترین تقریبهای عدد پی در نظر گرفته شده است.
حدود ۶۰۰ سال پس از ارشمیدس، ریاضیدان چینی به نام تسو چونگچی از روش مشابهی برای کشیدن چند ضلعی منتظم با ۱۲,۲۸۸ ضلع استفاده کرد. عدد پی محاسبه شده با این چندضلعی نزدیک به مقدار عدد کسری ۳۵۵/۱۱۳ و با دقت شش رقم اعشار پی بود. تقریبا ۶۰۰ سال دیگر طول کشید تا روش دیگری برای محاسبه دقیقتر پی ابداع شود.
محاسبه عدد پی به کمک سریهای بینهایت
سرانجام ریاضیدانان برای محاسبه عدد پی، فرمولهای دقیقی کشف کردند. تنها مشکل این فرمولها این است که برای رسیدن به دقیقترین تقریب پی باید آنها را تا بینهایت ادامه دهید که خب منطقی است؛ چون عدد پی هم تا بینهایت ادامه دارد.
یک نکته بسیار جالب در مورد عدد پی این است که برای محاسبه آن، تنها یک فرمول وجود ندارد و میتوان از راههای بسیاری مقدار تقریبی آن را به دست آورد. یکی از معروفترین و زیباترین این فرمولها، سری گرگوری-لایبنیتس (Gregory-Leibniz) است:
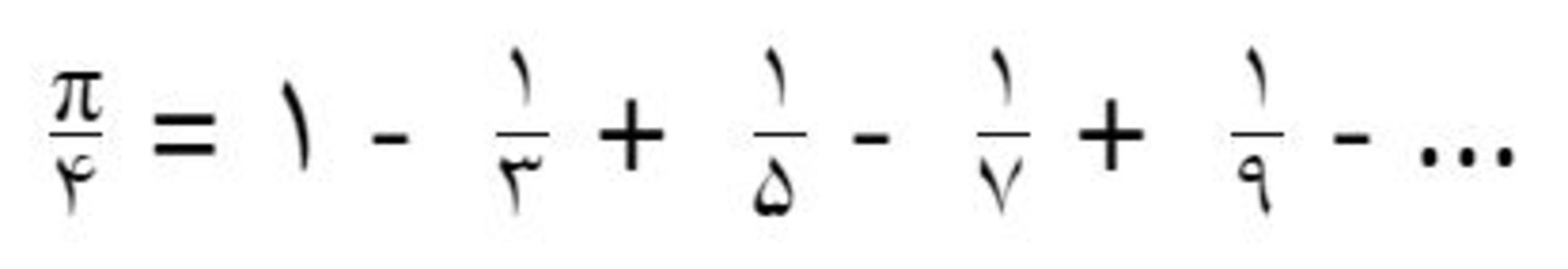
اگر میشد این الگو را تا ابد ادامه داد، آن وقت میتوانستیم مقدار دقیق π/۴ را محاسبه کرده و بعد برای بدست آوردن خود پی، این مقدار را در ۴ ضرب کنیم. مشکل این سری این است که برای رسیدن به عدد پی تنها تا دو رقم اعشار باید آن را تا ۳۰۰ واحد ادامه دهید!
فرمول دیگری که شما رو زودتر به جواب میرساند، سری نیلاکانتا (Nilakantha) است که در قرن پانزدهم میلادی ابداع شد:
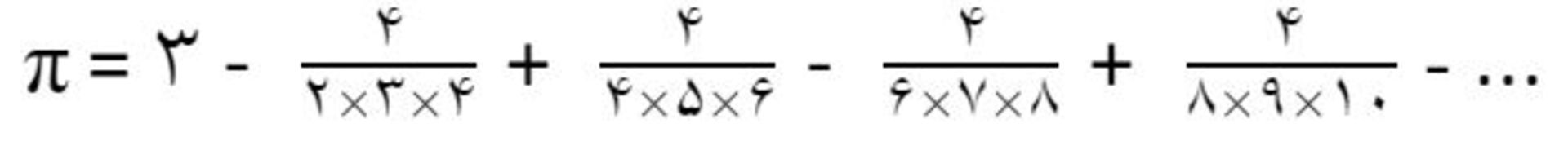
اما سریعترین فرمول محاسبه عدد پی، سری چودنوسکی (Chudnovsky) نام دارد که در همان اولین محاسبه، تا ۱۴ رقم اعشار پی را نشان میدهد. از این الگوریتم که در سال ۱۹۸۸ ابداع شد، حالا برای ثبت رکوردهای جهانی در محاسبات کامپیوتری استفاده میشود.
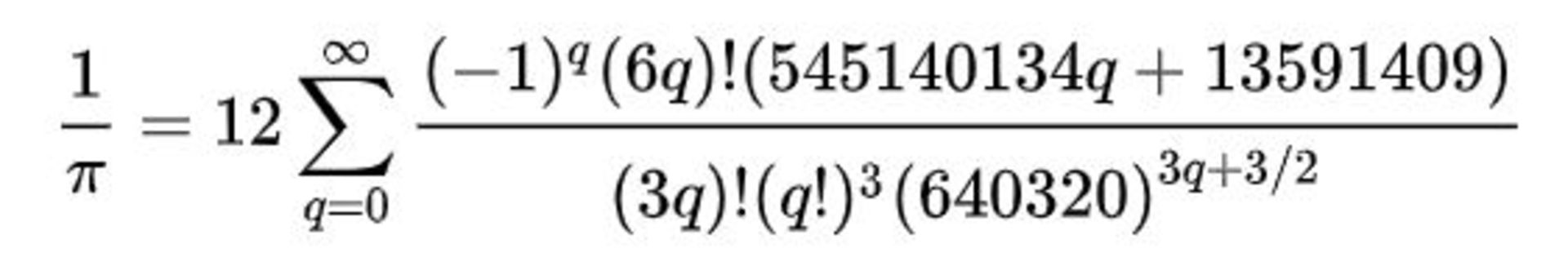
محاسبه دقیقتر و سریعتر عدد پی به کمک کامپیوتر
با گذر زمان، ریاضیدانان فرمولهای کارآمد دیگری را برای محاسبه عدد پی (π) ابداع کردند که برخی از آنها امروزه در محاسبات کامپیوتری استفاده میشود. مثلا به کمک همین الگوریتم چودنوسکی، گروهی از محققان در سال ۲۰۰۹ موفق شدند تا ۲٫۷ تریلیون رقم اشعار پی را در کامپیوتر محاسبه کنند. این محاسبات در سال ۲۰۲۰ به کمک این الگوریتم و نرمافزار y-cruncher به ۵۰ تریلیون رقم اعشار رسید.
حالا این ارقام را مقایسه کنید با محاسبات عدد پی قبل از ظهور کامپیوترها! در قرن نوزدهم، ویلیام شنکس برای محاسبه ۷۰۷ رقم اعشار پی، ۱۵ سال وقت گذاشت. متاسفانه، بعدها معلوم شد که او در این محاسبه دچار اشتباه شده و فقط تا ۵۲۷ رقم اعشار آن را درست حساب کرده است!
البته ما در بسیاری از محاسبات خود تنها به چند رقم اعشار پی نیاز داریم و آن ۹ یا ۱۰ رقم اعشاری که در ماشینحساب میبینید، احتمالا از سال ۱۴۰۰ میلادی شناخته شده بود.
اثبات گنگبودن پی
یکی از شگفتیهای عدد پی، گنگبودن آن است؛ اما همانطورکه هنوزهم برخی افراد فکر میکنند زمین تخت است، برخی نیز به گنگبودن عدد پی شک دارند. احتمالا مفاهیم اعداد گنگ و گویا را از ریاضی دوران مدرسه بهخاطر میآورید. اعدادی مثل ۳، ۰٫۵، ۰٫۳۳۳ یا ۱۰-، ۱/۲- یا ۱/۷ گویا هستند؛ چون تمام این اعداد را میتوان بهصورت کسری از اعداد صحیح (a/b) نوشت. ویژگی اعداد گویا این است که اعشار آنها جایی بهپایان میرسد (مثل ۲ٰ٫۲ یا ۱٫۴۱) یا بالاخره از جایی به بعد تکرار میشوند (مثل ۱/۳ که میشود ۰٫۳۳۳۳). درمقابل، اعداد گنگ را نمیتوان بهصورت کسری از اعداد صحیح نوشت. مثالهای معروف اعداد گنگ رادیکال ۲ و عدد اویلر (e = ۲٫۷۱۸۲۸) و البته همین عدد پی است.
اگرچه معمولا کسی به گنگبودن رادیکال ۲ شک نمیکند و تقریبا همه آن را بهعنوان واقعیتی در دنیای ریاضی پذیرفتهاند، دربارهی گنگبودن عدد پی سؤالات زیادی مطرح میشود. آیا واقعا هیچ پایانی برای پی نیست؟ آیا عدد پی چنان تا بینهایت ادامه دارد و تکراری نمیشود که میتوان هر زنجیره عددی مثلا شمارهتلفن خود را جایی در آن پیدا کرد؟
برای اثبات گنگبودن عدد پی چندین معادله مطرح شده است که شاید سادهترین آنها اثبات نیون (Niven) باشد که فرض میکند پی عددی گویا است؛ اما در آخر به تناقض میرسد. روش نیون برای اثبات گنگبودن عدد پی بر چهار مرحله زیر استوار است:
۱. فرض کنید پی عددی گویا است؛ یعنی π = a/b
۲. تابع f(x) را به شکل زیر تعریف کنید:
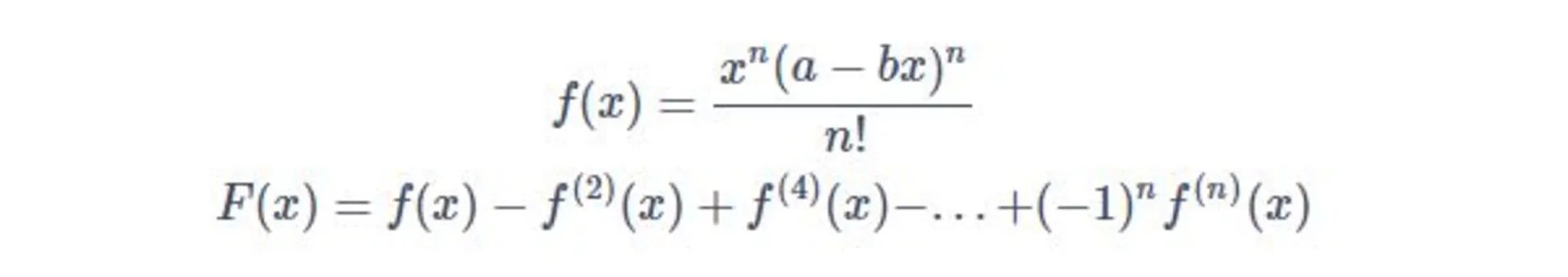
۳. بعد از کلی مرحله، ثابت کنید درصورت گویابودن عدد پی، انتگرال f(x) sin(x) از مقادیر ۰ تا پی، حتما عدد صحیح است.
۴. همزمان نشان دهید انتگرال f(x) sin(x) از مقادیر ۰ تا پی، مثبت خواهد بود؛ اما هرچه مقادیر n بزرگتر میشود، این مقدار به صفر متمایل میشود. تناقضی که به آن میرسید، این است: اگر جواب انتگرال عدد صحیح باشد، نمیتواند همزمان برابر با مقداری بین صفر و یک باشد.
بدینترتیب، اثبات میشود فرض اولیه اشتباه و پی عدد گنگ است. درواقع، اگر پی گویا باشد، مرحله چهارم میگوید جواب انتگرال میتواند بین صفر و یک باشد؛ اما مرحله سوم میگوید جواب همیشه باید عدد صحیح باشد. وجود این تناقض ثابت میکند پی نمیتواند گویا باشد.
تاریخچه عدد پی
دانشمندان و ریاضیدانان حداقل چهارهزار سال است که متوجه اهمیت عدد پی شدهاند. در کتاب تاریخ پی اثر پتر بکمان آمده است: «دوهزار سال قبل از میلاد بابلیها و مصریها از وجود و اهمیت ثابت π باخبر بودند و میدانستند نسبت محیط هر دایره به قطر آن یکسان است.» هم بابلیها و هم مصریها برای این ثابت، مقداری تقریبی در نظر گرفته بودند که بعدها ارشمیدس در یونان باستان آن را بهبود داد.
در قرن نهم میلادی، محمد خوارزمی، ریاضیدان شهیر ایرانی، عدد پی را تا چهار رقم اعشار دقیق محاسبه کرد. در قرن پانزدهم میلادی نیز، غیاثالدین جمشید کاشانی، ریاضیدان شهیر ایرانی، توانست مقدار ۲π را تا شانزده رقم اعشار محاسبه کند؛ بهطوریکه تا ۱۵۰سال بعد، کسی نتوانست آن را بیش از این بسط دهد.

در قرون بعدی، ریاضیدانان چینی و هندی و عرب بهجای بهبود روش ارشمیدس، تعداد ارقام اعشاری پی را با انجام محاسبات سخت و طاقتفرسا افزایش دادند. در پایان قرن هفدهم، روشهای محاسبات ریاضی در اروپا بهبود یافت و فرمول بهتری برای محاسبه سری بینهایت عدد پی معرفی شد. بهعنوان مثال، اسحاق نیوتن از قضیه بسط دوجملهای خود برای محاسبه سریع ۱۶ رقم اعشار پی استفاده کرد. در اوایل قرن بیستم، سرینیواسا رامانوجان، ریاضیدان هندی، روشهای فوقالعاده کارآمدی برای محاسبه پی ابداع کرد که بعدا در الگوریتمهای کامپیوتری بهکار رفتند.
اولین کسی که فهمید نسبت محیط دایره به قطر عددی گنگ است، یوهان لمبرت، ریاضیدان سوئیسی بود که سال ۱۷۶۸ نشان داد محاسبه مقدار دقیق پی غیرممکن است؛ چون اعشار این عدد تا بینهایت ادامه دارد.
افزونبراین، اولین کسی که تصمیم گرفت برای این عدد گنگ نماد π را انتخاب کند، ویلیام جونز، ریاضیدان اهل پادشاهی انگلستان بود که π را از کلمه یونانی بهمعنی «محیط» انتخاب و آن را در کتابش معرفی کرد. بااینحال، سی سال طول کشید تا استفاده از π بهعنوان ثابت پی متداول شود. درواقع، کسی که باعث شهرت نماد π شد، لئونارد ایولر، ریاضیدان سوئیسی بود که در دهه ۱۷۳۰ از این نماد در مقالاتش در قضیه مثلثات استفاده کرد.
با شروع قرن بیستم، حدود ۵۰۰ رقم پی محاسبه شده بود. با پیشرفت تکنولوژی و بهلطف محاسبات کامپیوتری، اکنون ما تا دَهها تریلیون رقم اول پی را میدانیم. در سال ۲۰۱۹، اِما هاروکا، مشاور توسعه فضای ابری در گوگل، موفق شد با استفاده از ۱۷۰ ترابایت داده و برنامه چندرشتهای موسوم به y-cruncher، دقیقترین مقدار عدد پی در جهان را محاسبه کند که شامل ۳۱٫۴ تریلیون رقم اعشار میشد. محاسبه این ارقام ۱۲۱ روز طول کشید. سال ۲۰۲۰ رکورد محاسبه بیشترین ارقام پی به ۵۰ تریلیون رسید.
عدد پی کامل
همانطورکه گفته شد، پی عدد گنگ است؛ یعنی نمیتوان آن را بهصورت کسری ساده با اعداد صحیح بیان کرد. دلیلش هم این است که پی طبق توصیف ریاضیدانان «اعشار بینهایت» است؛ یعنی ارقام بعد از ممیز تا ابد ادامه خواهند یافت و به هیچ رقمی ختم نمیشوند.
اگرچه برای پی مقدار دقیقی وجود ندارد و برای اکثر محاسبات تا حدود سی رقم اعشار کافی است، بسیاری از ریاضیدانان و ریاضیدوستان همچنان مشتاق هستند تا عدد پی را تا بیشترین رقم ممکن محاسبه کنند. یکی از دلایل این اشتیاق ثبت رکورد و مشهورشدن است. دانشمندان هم با بسط سری اعشار پی، از آن برای آزمودن اَبَرکامپیوترها و الگوریتمهای تجزیهوتحلیل اعداد استفاده میکنند.
رکورد جهانی گینس برای خواندن بیشترین ارقام پی بهصورت ذهنی درحالحاضر متعلق به راجویر مینا هندی است که سال ۲۰۱۵، با چشمان بسته موفق شد تا ۷۰ هزار رقم اعشار پی را از حفظ بخواند. برخی برنامهنویسان کامپیوتر هم توانستهاند بهکمک الگوریتمهای خاصی تا ۵۰ تریلیون رقم اعشار پی را محاسبه کنند. عدد پی تا ۱۰۰ رقم اعشار بدینصورت محاسبه شده است:
۳٫۱۴۱۵۹ ۲۶۵۳۵ ۸۹۷۹۳ ۲۳۸۴۶ ۲۶۴۳۳ ۸۳۲۷۹ ۵۰۲۸۸ ۴۱۹۷۱ ۶۹۳۹۹ ۳۷۵۱۰ ۵۸۲۰۹ ۷۴۹۴۴ ۵۹۲۳۰ ۷۸۱۶۴ ۰۶۲۸۶ ۲۰۸۹۹ ۸۶۲۸۰ ۳۴۸۲۵ ۳۴۲۱۱ ۷۰۶۷
دیدن عدد کامل پی ممکن نیست؛ چون این عدد تا بینهایت ادامه دارد؛ اما میتوانید این عدد را تا یکمیلیون رقم اعشار در وبسایت piday.org مشاهده کنید.
معمای اعداد گنگ؛ چرا «پی» تمام نمیشود؟
چرا ارقام «پی» تا ابد ادامه دارند؟ آیا سادهتر نبود که «پی» دقیقاً ۳، یا ۳٫۵، یا حتی ۳٫۱۴ باشد؟ ما «پی» را انتخاب نمیکنیم؛ «پی» بخشی از مکانیک طبیعت است، ما فقط آن را کشف کردهایم.
اگر در هر ثانیه یک رقم بخوانید، ۱٫۵ میلیارد سال طول میکشد تا ۵۰ تریلیون رقم پی را تمام کنید
اول، باید یک تصور غلط رایج را اصلاح کنیم: مردم اغلب میگویند «پی بینهایت است»؛ درحالیکه «پی» یک عدد متناهی و محدود است (میدانیم که جایی بین ۳ و ۴ قرار دارد). چیزی که بینهایت است، تعداد ارقام اعشاری آن است.
اعداد زیادی هستند که ارقام اعشاری بینهایت دارند. برای مثال، کسر «یکسوم» (۱/۳) که مساوی است با ...۰٫۳۳۳۳ و سهها تا ابد ادامه دارند. اما تفاوت بزرگی وجود دارد. اعدادی مانند یکسوم، گویا نامیده میشوند. یعنی میتوان آنها را به صورت کسر دو عدد صحیح نوشت و ارقام اعشاری آنها یا تمام میشوند (مثل ۰٫۵) یا به صورت یک الگوی مشخص تکرار میشوند (مثل ...۰٫۳۳۳).
اما «پی» متفاوت است. پی یک عدد گنگ است، به این معنی که ارقام اعشاری آن نهتنها تا ابد ادامه دارند، بلکه هرگز تمام نمیشوند و هرگز در یک الگوی مشخص تکرار نمیشوند.
به همین دلیل است که ما به نماد «π» احتیاج داریم. لحظهای که شما از نوشتن ارقام «...۳٫۱۴۱۵۹» دست میکشید، دیگر «پی» را ننوشتهاید، بلکه فقط تقریبی از آن را نوشتهاید.
شاید فکر کنید این اعداد گنگ، کمیاب هستند، اما دقیقاً برعکس، بیشتر اعداد، گنگ هستند. اگر اعداد گویا مانند ستارههای پرشمار در آسمان شب باشند، اعداد گنگ، تاریکی مطلق و بیکران میان آن ستارگان هستند.
اصلاً چرا به محاسبه عدد پی اصرار داریم؟
امروزه ما بهلطف کامپیوترها، تریلیونها رقم «پی» را میدانیم. و این سوال اساسی را مطرح میکند: «اصلاً چرا؟»
واقعیت این است که اکثر مهندسان در محاسبات خود نهایتاً از چهار یا پنج رقم «پی» استفاده میکنند. دانستن رقم دههزارم پی به ما کمک نمیکند پلهای محکمتری بسازیم یا خودروهای سریعتری طراحی کنیم. شاید تنها کاربرد عملی محاسبهی تریلیونها رقم پی، برنده شدن در مسابقات حفظ پی» باشد که رکورد جهانی آن ۷۰,۰۰۰ رقم با چشمان بسته است!
اما ریاضیدانان نمیتوانند در برابر چالش مقاومت کنند. ارزش واقعی این تلاشها، خودِ آن تریلیونها رقم نیست، بلکه روشهایی است که برای رسیدن به آنها ابداع کردهایم.
همان فرایند تکرارشوندهای که ارشمیدس برای محاسبهی پی ابداع کرد، درواقع سنگبنای اولیه حساب دیفرانسیل و انتگرال بود. بسیاری از شاخههای ریاضی با یک کنجکاوی ساده شروع میشوند و سالها یا قرنها بعد، کاربردهای عملی شگفتانگیز آنها در دنیای واقعی آشکار میشود.
اگر میتوانستیم ارشمیدس را از مرگ بازگردانیم و دنیای قرن بیستویکم را به او نشان دهیم، آیا هرگز باور میکرد که کار او بر روی چندضلعیهای درون دایره، نقشی حیاتی در فناوریهایی ایفا کرده که حتی در رویاهایش هم نمیگنجید؟
کاربرد عدد پی در طبیعت
کاربرد عدد پی را میتوان در طبیعت بهوفور پیدا کرد. درواقع، هرجایی در طبیعت که شکل دایره وجود دارد، مثل قرص خورشید و ماه، مارپیچ دوگانه DNA، مردمک چشم و حلقههای متحدالمرکزی که از افتادن جسمی درون آب ایجاد میشوند، عدد پی آنجا حضور دارد و در محاسبات بهکار میرود.
عدد پی در فیزیک مربوط به توصیف امواج، ازجمله نور و صدا نیز بهکار میرود. حتی در معادلهای که وضعیت دقیق جهان را بررسی میکند، یعنی اصل عدم قطعیت هایزنبرگ که میگوید نمیتوان همه کمیتهای یک الکترون را همزمان اندازهگیری کرد، میتوانید رد عدد پی را بیابید.
پی در شکل رودخانهها هم ظاهر میشود. رودخانههایی که از سرچشمه تا دهانه مسیر مستقیمی را طی میکنند، نسبت مئاندری یا پیچان کوچکی دارند؛ درحالیکه رودخانههایی که در طول مسیر بهطور مارپیچ حرکت میکنند، نسبت مئاندری بیشتری دارند. میانگین نسبت مئاندری رودخانهها تقریبا برابر با عدد پی است و این نکته جالب را اولینبار آلبرت انیشتین با استفاده از دینامیک سیالات و نظریه آشوب توضیح داد.
ثابت π به پیدایش روش جدیدی برای اندازهگیری زاویه (رادیان) نیز انجامید که به درک بهتر ما از جهان کمک بسیاری کرد. شاید عدد پی در کارهای روزمره ما بهکار نرود؛ اما در اکثر محاسبات مربوط به ساختوساز، فیزیک کوانتومی، ارتباطات، نظریه موسیقی، جراحی پزشکی، سفرهای هوایی و فضایی کاربرد دارد. درواقع، ناسا بهطور مرتب از عدد پی برای محاسبه مسیر فضاپیماها استفاده میکند. کاربردهای دیگر عدد پی در ناسا شامل تعیین اندازه دهانههای برخوردی و سیارههای خارج از منظومه شمسی، تعیین میزان پیشرانه برای فضاپیماها و مواد سازنده سیارکها میشود.

عدد پی در دنیای تکنولوژی هم کاربردهای زیادی دارد. بسیاری از نرمافزارهای تشخیص صدا برای گرفتن «اثرانگشت» از طیف قدرت صدا و تشخیص کلمات کاربر، بر تبدیل فوریه (Fourier transform) متکی هستند که از عدد π استفاده میکند. گوشی موبایل برای برقراری ارتباط با برج مخابرات و حتی گوش انسان برای تشخیص صدای افراد از تبدیل فوریه استفاده میکند که درواقع، توابع زمان یا فضا را به توابعی برحسب فرکانس زمانی یا فضایی تبدیل میکند.
علاوهبراین، وقتی سراغ رادیو میرویم و برای گوشدادن به موج خاصی پارامترهای مدار الکتریکی را طوری تنظیم میکنیم تا با فرکانس سیگنال پخش همگام شود، بازهم با عدد پی سروکار داریم. عدد پی کاربردهای بسیاری در علوم نوین دارد و روزانه در میلیاردها محاسبه ازجمله شبیهسازی آبوهوا در اَبَرکامپیوترهای عظیم بهکار برده میشود. بدون شک، با پیشرفت تکنولوژی استفاده از عدد پی در آینده بیشتر خواهد شد.
روز جهانی عدد پی
در وصف اهمیت عدد پی همین بس که روزی برای بزرگداشت آن در تقویم ثبت شده است. آمریکا ۱۴ مارس (۲۴ اسفند) را روز جهانی عدد پی انتخاب کرده و دلیل نامگذاری این روز آن است که در آمریکا فرمت نوشتن تاریخ بهترتیب ماه و روز و سال است و ۱۴ مارس بهصورت ۳٫۱۴ یعنی همان عدد پی نوشته میشود. نکته جالب اینکه آلبرت انیشتین روز پی بهدنیا آمد و استیون هاوکینگ، فیزیکدان نظری، هم ۱۴ مارس ۲۰۱۸ درگذشت.
سال ۱۹۸۸، لری شاو، فیزیکدان نامآشنا، اولینبار روز عدد پی را در موزه علمی اکسپلوراتوریوم واقع در سانفرانسیسکو جشن گرفت. تا سال ۲۰۰۹، مراسم بزرگداشت این روز آنقدر محبوب شده بود که کنگره آمریکا برای رسمیکردن آن لایحهای تصویب کرد و از مدارس و معلمان سراسر دنیا خواست این روز را با انجام فعالیتهای مناسب و سرگرمکننده جشن بگیرند و به دانشآموزان اهمیت عدد پی و ریاضیات را بیاموزند. سال ۲۰۱۰ نیز، گوگل دودل بهمناسبت سیامین سالگرد روز پی طرحی متناسب با این روز منتشر کرد.
روز پی فرصتی است تا علاوهبر اندیشیدن به آثار و تلاشهای ریاضیدان تاریخ برای محاسبه هرچه دقیقتر این عدد، فعالیتهای سرگرمکنندهای مثل پختن و خوردن کیک پای، حفظکردن ارقام پی و تماشای فیلمهایی با موضوع عدد پی یا ریاضی (مثل فیلم «ذهن زیبا»، «پی» یا «نظریه همهچیز») انجام دهیم. تفریح دیگری که در این روز میتوان انجام داد، نوشتن «پای-کو» است که درواقع نسخه ریاضی شعر سنتی هایکو است. درحالیکه هایکو شعر ژاپنی سهبیتی با الگوی هجایی ۵-۷-۵ است، شعر «پای-کو» از الگوی هجایی ۴-۱-۳ پیروی میکند.
تاریخهای دیگری که برای بزرگداشت عدد پی در نظر گرفته شده، ۲۲ جولای (۲۲/۷) رقم تقریبی پی و ۲۸ ژوئن (۲۸/۶) عدد تقریبی 2π معادل با ۳۶۰ درجه است.
معجزات عدد پی
ویژگیهای عدد پی گاهی آنقدر شگفتانگیز است که برخی افراد از آنها بهعنوان «معجرات» عدد پی یاد میکنند. درادامه، به بعضی از این ویژگیها اشاره میکنیم.
عدد پی تا بینهایت ادامه دارد
پی عدد گنگ است و نمیتوان آن را بهشکل کسری از اعداد صحیح نوشت؛ بههمیندلیل، اعشار این عدد نه الگوی تکراری دارد و نه بعد از رقمی تمام میشود. درواقع، رقمهای بعد از ممیز عدد پی تا بینهایت ادامه دارند. درحالحاضر، تا ۵۰ تریلیون رقم پی محاسبه شده؛ اما این پایان داستان نیست و هنوز افراد زیادی بهکمک کامپیوترهای قدرتمند میکوشند این رکورد را بشکنند.
رقمهای اعشار پی کاملا تصادفی هستند
یکی از «معجزات» عدد پی این است که ارقام اعشاری آن تا بینهایت بهصورت الگوهایی کاملا تصادفی ادامه پیدا میکنند. ریاضیدانان قرنها بهدنبال مشاهده الگویی در این ارقام بودهاند تا اینکه سال ۱۷۶۸، یوهان لمبرت، ریاضیدان و ستارهشناس سوئیسیآلمانی، اثبات کرد پی عددی گنگ است و زنجیره اعداد آن هیچ الگوی مشخصی ندارند.
در پی میتوان هر رشته عددی مثل شمارهتلفن خود را پیدا کرد
داستان معروفی وجود دارد که میگوید «پی» شامل هر توالی عددی قابل تصوری است. یعنی شماره تلفن شما، تاریخ تولدتان، یا حتی متن کامل کتابها (اگر به عدد تبدیل شوند) جایی در میان ارقام «پی» پنهان شدهاند.
شماره تلفن شما، تاریخ تولدتان یا متن کامل کتابها احتمالاً جایی در میان ارقام پی پنهان شدهاند
این ایده به این بستگی دارد که ارقام پی دارای «توزیع تصادفی یکنواخت» باشند. تا جایی که ما با تریلیونها رقم محاسبه شده بررسی کردهایم، ارقام پی قطعاً به نظر میرسد که تصادفی هستند. اما «تصادفی به نظر رسیدن» با «تصادفی بودن» دو چیز متفاوت است. مورد دوم به استاندارد بسیار بالاتری از اثبات ریاضی نیاز دارد.
پاتریک اینگرم، ریاضیدان دانشگاه یورک در تورنتو، دراینباره میگوید: «این موضوع هنوز اثبات نشده است؛ اما در حد نظریه، اگر رشتهای از میلیونها عدد داشته باشید، سری اعداد موردنظر شما بالاخره جایی در آن پیدا میشود و دوباره هم پیدا میشود تا بینهایت.»
برای امتحان درستی این موضوع میتوانید رشته عددی مدنظرتان را در موتور جستوجوی عدد پی تایپ کنید و ببینید آیا این اعداد با این چینش در پی آمدهاند یا خیر. البته بهیاد بسپارید که این موتور جستوجو فقط تا ۲۰۰ میلیون رقم پی را بررسی میکند و اگر رشته عددی شما در آن یافت نشد، احتمالا در رقمهای بیشتر وجود دارد.
تاکنون بیش از ۵۰ تریلیون اعشار پی محاسبه شده و داستان هنوز ادامه دارد
درست است که برای پی هیچ انتهایی تعریف نشده است؛ اما ما انسانها هیچگاه از تلاش برای محاسبه ارقام آن دست برنداشتهایم. زمانی ریاضیدانان فقط میتوانستند تا ۱۰ رقم اعشار پی را محاسبه کنند؛ اما اکنون بهکمک الگوریتمهای کامپیوتری توانستهایم تا ۵۰ تریلیون رقم اعشار پی را بهدست آوریم. سال ۲۰۲۰، تیموتی مولیکان بعد از دَه ماه رایانش طاقتفرسا در کامپیوتر شخصی قدیمی، اما قدرتمندش توانست رکورد پی محاسبهشده را بشکند. تیموتی برای محاسبه ۵۰ تریلیون رقم اعشار پی از کامپیوتر Ivy Bridge ساخت و سال ۲۰۱۲ از آن بههمراه ۴۸ هارددرایو ییشرفته استفاده کرد.
برای اینکه درک کنید محاسبه ۵۰ تریلیون عدد چقدر شگفتانگیز است، به این فکر کنید که اگر در هر ثانیه یک رقم بخوانید، بیش از ۱٫۵ میلیارد سال طول خواهد کشید تا خواندن تمام این ۵۰ تریلیون رقم را تمام کنید.
انسانها میتوانند هزاران رقم اعشار پی را از حفظ بخوانند
درحالحاضر، رکورد حفظ بیشترین رقم اعشار پی متعلق به مردی هندی به نام سروش کومار شارما است که سال ۲۰۱۵ توانست ۷۰،۰۳۰ رقم پی را در ۱۷ ساعت و ۱۴ دقیقه از حفظ بخواند و به صدر فهرست ردهبندی جهانی پی راه پیدا کند. پیش از او، مرد هندی دیگری به نام راجویر مینا تا دَه سال این رکورد را برای ۷۰ هزار رقم اعشار حفظ کرده بود. فردی از ژاپن به نام آکیرا هاراگوچی مدعی است ۱۰۰ هزار رقم پی را در رویدادی در توکیو در سال ۲۰۰۶ از بَر خوانده؛ اما تابهحال در هیچ فهرست رسمی نامش را ثبت نکرده است.
هرجا در طبیعت شکل دایره باشد، عدد پی آنجا حضور دارد
خوشبختانه برای حفظکردن ارقام پی به استعداد خاصی در ریاضی نیازی نیست. شارما قبلا سبزیفروش بود و امتحان ورودی مهندسی دانشگاه را هم رد شد. بااینحال، او توانست تمام این ۷۰ هزار رقم را با ربطدادن هر رقم به تصویری خاص حفظ کند. شارما حالا دیگران را برای تقویت حافظه آموزش میدهد.
مردی در آمریکا به نام مارک اومیل سال ۲۰۰۷ موفق شد ۱۵ هزار رقم پی را از حفظ بخواند. او گفت روشش برای حفظ این ارقام بدینصورت بود که آنها را از روی کاغذ بلند میخواند و صدای خود را ضبط میکرد. بعد بارهاوبارها به صدای ضبطشدهاش گوش میکرد تا آنها را بهخاطر بسپارد. او گفت سندروم آسپرگر هم در این زمینه به او کمک کرد.
حتی مهندسان موشکی نیز فقط به کمی بیش از دَه رقم اعشار پی نیاز دارند
اگرچه کامپیوترهای قدرتمند توانستهاند تریلیونها رقم اعشار پی را محاسبه کنند، ما انسانها واقعا به تمام آنها نیازی نداریم. حتی مهندسان ناسا هم برای محاسبه مدارهای سیارهها تا پانزده رقم اعشار پی را در نظر میگیرند.
درواقع، اگر میخواستید اندازه جهان مشاهدهشدنی را محاسبه کنید، استفاده از تنها ۳۹ رقم پی در معادلات جوابی به شما میداد که فقط بهاندازه اتم هیدروژن با اندازه واقعی جهان اختلاف داشت. بهعبارتدیگر، هیچ محاسبه واقعی در دنیای فیزیکی وجود ندارد که دانشمندان برای انجامش بخواهند به تعداد بیشتری از این ارقام پی احتیاج داشته باشند.
پی زبان مخصوص خود را دارد: پایلیش
برای عدد پی زبان مخصوصی به نام «پایلیش» (Pilish) ابداع شده که در آن، تعداد حروف هر کلمه متناسب با ترتیب ارقام پی است. نوشتن به زبان پایلیش بسیار سخت است؛ بااینحال، ریاضیدانی به نام مایکل کیث توانسته رمان کوتاهی را تا دَههزار رقم اعشار پی بنویسد. برای مثال، در فارسی جمله خرد | و | دانش | و | آگاهی | دانشمندان | ره | سرمنزل | مقصود | بما | آموزد به زبان پایلیش نوشته شده و از الگوی ۵-۳-۵-۶-۲-۹-۵-۱-۴-۱-۳ پیروی میکند.
عدد 3.14 در آینه شبیه کلمه PIE بهنظر میرسد
راز شهرت پی
چرا ما اینقدر شیفتهی «پی» هستیم؟ دلیل این شیفتگی صرفا بهخاطر ارقام بینهایت و تکرارنشدنیاش نیست.
شاید پاسخ، در رازآلود بودن آن نهفته است. پی نماد ۴۰۰۰ سال تلاش، کنجکاوی و مبارزهی فکری بشر برای درک چیزی است که به نظر ساده میآمد، اما درنهایت، دستنیافتنی بود. ما فهمیدیم که هر تلاشی برای نوشتن کامل عدد پی، محکوم به شکست است، زیرا هرگز نمیتوانیم بینهایت رقم را بنویسیم.
و شاید، شهرت پی بیش از هر چیز به شهرت دایره گره خورده است.
وقتی برای اولین بار اشکال هندسی را یاد میگیریم، دایره را همزمان با مربع و مثلث میآموزیم. اما اگر عمیقتر فکر کنید، دایره در طبیعت بسیار بنیادیتر از مربع و مثلث است. شما چند مربع کامل در طبیعت میبینید؟ اما دایرهها همهجا هستند: در چشمان ما، در آسمان، در سر گلها، در مقطع تنه درختان و در امواجی که از افتادن یک قطره باران در آب ساکن ایجاد میشوند.
پی در معادلات فیزیک، در مکانهایی ظاهر میشود که هرگز انتظارش را ندارید. چون در اعماق آن قوانین فیزیک، دایرههایی پنهان شدهاند.
پی از این جهت مشهور است که امضای یکی از اساسیترین، ابتداییترین و در عین حال عمیقترین اشکال موجود در جهان ماست.
این مطلب در تاریخ ۲۶ آبان ۱۴۰۴ بهروز شد.



