پیدایش مکانیک ماتریسی و مناظره بزرگان

در قسمت‌های قبلی، بررسی جامعی از بخش‌های مختلف فیزیک نوین، نظیر نسبیت، ساختار‌های اتمی، قانون پلانک و ... داشتیم. همان‌طور که در قسمت قبل گفتیم، اکنون وارد نسل دوم فیزیکدانان کوانتومی شده‌ایم و از قضا بخش اعظمی از تحولات مکانیک کوانتومی در همین دوره صورت می‌گیرد. ورنر هایزنبرگ یقینا یکی از بزرگ‌ترین فیزیکدانان معاصر و شاید جزو پنج شخصیت تاثیر گذار بر جریان فیزیک کوانتومی باشد. در این قسمت، بررسی جامعی بر تاثیرگذاری او بر جریان فیزیک جدید داریم.

پیش از شروع این قسمت، به‌عنوان نگارنده این مطلب بر خود لازم می‌دانم تا توضیحاتی را ارائه دهم؛ همان‌طور که از همان ابتدای شروع این مقالات نیز بیان کردیم، هدف از جمع‌آوری این مجموعه‌ ارائه‌ی اطلاعاتی جامع و کامل برای مخاطبی است، که به فیزیک علاقه‌مند است، اما دانش ریاضی کافی را ندارد. به همین منظور پله پله با پیچیده‌تر شدن مطالب و ورود به مباحث کوانتومی دغدغه و مشغولیت ذهنی ما نیز به منظور ساده ارائه دادن موضوعات بیشتر و بیشتر می‌شد و در هر قسمت با پیداکردن منابع و مطالب مختلف که محاسبات ریاضی را به‌نوعی دور زده بودند، به جمع آوری مطالب و گردآوری آن می‌پرداختیم. قسمتی که با آن روبه‌رو هستید، طولانی‌تر از تمامی قسمت‌های پیشین است و شاید بد نباشد در همین ابتدا بدانید که با مقاله‌ای روبه‌رو هستید که نزدیک به ۱۸ هزار کلمه محتوا دارد و کار نگارش و جمع‌آوری آن نزدیک به یک ماه طول کشیده است. با این وجود تمامی سعی بر این بوده است، که موضوع به‌حدی جذاب باشد که شما گذر زمان و گستردگی مطالب را احساس نکنید. هایزنبرگ یکی از معدود دانشمندانی است، که در هنگام حیاتش کتابی به قلم خود، مبتنی بر شرح حوادثی که در طول سالیان بر او رخ داده است، نوشته است  نام این کتاب Physic And Beyond است و در کشورمان با نام جز و کل ترجمه و منتشر شده است. همین موضوع کمک به شایانی به تمامی روایتگران علم می‌کند، چرا که منبعی مستند و بی‌واسطه در اختیار دارند. در بخش‌های متعددی از این مقاله مناظره و بحث‌های دانشمندان بزرگ نظیر اینشتین، بور، دیراک، پائولی و ... را با یکدیگر حول فیزیک کوانتوم شاهد هستیم، بحث‌ها و صحبت‌هایی که خواندنشان مملو از جذابیت و نکات آموزشی و در عین حال اخلاقی است.

باتوجه‌به حجم بالای مطالب، ابتدا در نظر داشتم، این مقاله را به چند قسمت، تقسیم کنم، اما باتوجه‌به پیوستگی بیش از حد مطالب و بحث‌هایی که کاملا مربوط و پی در پی یکدیگر هستند، تصمیم گرفتم این مقاله را در یک قسمت، منتشر کنم، اما برای راحتی خواننده، مقاله را به سه بخش پیشنهادی تقسیم کرده‌ام، پیشنهاد من این است که پس از مطالعه‌ی هر قسمت، یک روز به خود زمان دهید و قسمت بعدی را در روز بعد بخوانید، این‌گونه فهم و هضم مطالب نیز برای شما راحت‌تر و مفیدتر خواهد بود. همان‌طور که می‌دانید در زومیت، قابلیتی به‌عنوان ذخیره کردن مقالات وجود دارد، بنابراین اگر مایل به خواندن پیوسته این قسمت هستید، این مقاله را در صفحه شخصی خود ذخیره کنید، تا در روزهای آینده که برای خواندن بخش‌های بعدی می‌آیید، کارتان برای پیدا کردن مقاله ساده باشد.

پس از مقدمه‌ای نسبتا طولانی، حال وقت آن است که به معرفی اجمالی و شرحی کلی بر ورنر هایزنبرگ بپردازیم. 

ورنر هایزنبرگ، فیزیکدان آلمانی که مهارت او در پدید آوردن نظریه‌های گسترده و دامنه دار، باعث تولد مکانیک ماتریسی شد. (چند ماه پیش از آن که شرودینگر ایجادکننده مکانیک موجی باشد) اواخر سال ۱۹۰۱ در دورتسبورگ آلمان چشم به جهان گشود. در آن هنگام، پدر ورنر در دبیرستان آلتس در وورتسبورگ زبان‌های باستانی تدریس می‌کرد. او در سال ۱۹۱۰ به کرسی مهم زبان شناسی یونان در دانشگاه مونیخ منصوب شد.

در سال‌های تعیین کننده نوجوانی هایزنبرگ، اروپا در جنگ جهانی اول پاره پاره شده بود. در آشوب‌های سیاسی و اقتصادی پس از جنگ، پیر و جوان آلمانی سرگردان و مأیوس بودند. هایزنبرگ در زندگینامه شخصی خود می نویسد:

زمام و قدرت از دست‌های یک نسل پیرتر عمیقا سرخورده و مایوس ساقط شده بود و جوان‌ترها کنارهم در تلاش بودند، تا چراغ راه‌های نوینی را روشن نگهدارند، یا دست کم ستاره‌ی جدیدی را کشف کنند، تا راهنمای گام‌های آنان در تاریکی غالب و فراگیر باشد.

 هایزنبرگ ستاره‌ی راهنمایش را در ایده‌های رومانتیک یا آرمان‌های رویایی نهضت جوانان موسوم به پیش‌آهنگان جدید آلمان یافت، او رهبر گروهی از پسران جوان‌تر شد، که تبدیل به دوستانی صمیمی برای باقی عمر او شدند. آنان پیاده‌روی و کوهنوردی می‌کردند، اردو می‌رفتند و به‌طور جدی و صمیمانه درباره‌ی آینده آلمان به گفت و گو می‌پرداختند.

اگوست هایزنبرگ؛ پدر او با معرفی تأملات فیلسوف دانشمندان یونانی به تعلیمات علمی پسرش کمک می‌کرد و به اندوخته‌های علمی فرزند خود می‌افزود، به طوری که پسرش نوشته‌های علمی یونانیان را باورپذیرتر از کتاب‌های درسی‌اش یافت. هایزنبرگ درحالی‌که هنوز جوان بود، مانند؛ بولتزمن، پلانک و اینشتین یک موسیقیدان ماهر شد.

 ابتدا می‌خواست یک پیانیست شود، اما ابداعات اینشتین برای او نزدیک‌تر و جذاب‌تر از ابداعات موتزارت به نظر می‌رسید. ازاین‌رو در سال ۱۹۲۰، او در سن نوزده سالگی، خودش را به آرنولد زومرفلد در دانشگاه مونیخ، به‌عنوان یک دانشجوی احتمالی فیزیک نظری معرفی کرد.

حضور خشک و جدی زومرفلد، تا حدی مانند پلانک، گیرا و اثر گذار اما مرعوب‌کننده نبود. هایزنبرگ چنین به خاطر می آورد؛

او مردی کوچک اندام، چاق و قوزدار با سبیل سیاه چخماقی و تا حدی عبوس و سخت‌گیر به نظرم می‌رسید، اما از همان نخستین جملاتش، خیرخواهی او، توجه و علاقه صادقانه‌اش نسبت به جوانان آشکار شد، به‌خصوص برای پسری که آمده بود، تا از راهنمایی و توصیه‌های او برخوردار شود.

 هایزنبرگ جوان به‌تازگی از دبیرستان فارغ التحصیل شده بود و به دشواری پیشنهادی که مطرح می‌کرد آگاهی و اعتنایی نداشت. او به زومرفلد گفت، که می‌خواهد درباره‌ی نظریه‌ی نسبیت عام اینشتین(به شکلی مفصل در قسمت چهارم این مجموعه مقالات بررسی شده است) تحقیق کند و آن را توسعه دهد. زومرفلد به او اجازه داد، در سمینار پیشرفته حضور یابد، اما دوره‌هایی از برنامه فیزیک استاندارد را نیز به او توصیه کرد.

روزی هنگام ورود به سالن سخنرانی زومرفلد، ورنر هایزنبرگ دانشجویی سیاه موی با چهره‌ای نسبتا مرموزی را مشاهده کرد، این شخص ولفگانگ پائولی بود که بعدها تبدیل به دوست نزدیک هایزنبرگ شد. پائولی در مورد فعالیت زومرفلد برای بسط نظریه‌ی اتمی بور نظر مساعدی نداشت و آن را یک آشفتگی بزرگ می‌دانست.

نقطه‌ی اوج آموزش هایزنبرگ در فیزیک، طی چهارمین نیمسال تحصیل او زمانی حاصل شد، که زومرفلد دانشجوی باهوش و زرنگ خود را به گوتینگن بُرد، تا در یک سری از سخنرانی‌هایی که نیلز بور درباره‌ی نظریه اتمی ایراد می‌کرد، شرکت کند. موقعیتی که دانشجویان آن را فستیوال بور می‌نامیدند. خاطرات هایزنبرگ از این سخنرانی‌ها نشان از اثری مسیحایی دارد، که بور درون او ایجاد کرده است؛

من هرگز نخستین سخنرانی را فراموش نمی‌کنم. ظرفیت سالن پر شده بود. فیزیکدان بزرگ دانمارکی، که همان قد و قامتش اسکاندیناوی بودنش را نشان می‌داد، دربرابر تریبون ایستاده بود. سرش اندکی خمیده بود و لبخندی دوستانه اما تا حدی نگران بر لب داشت. نور تابستانی از پنجره‌های کاملا باز سیل آسا به درون می‌تابید. بور کاملا آرام با لهجه‌ی اندکی دانمارکی صحبت می‌کرد. وقتی تک تک مفروضات نظریه‌اش را توضیح می‌داد، کلمات را بسیار دقیق، بسیار دقیق‌تر از بیان معمولی زومرفلد انتخاب می‌کرد و هر یک از جمله‌های دقیقا انتخاب شده‌اش، سلسله‌ی طویلی از افکار زیر بنایی بازتاب‌های فلسفی را آشکار می‌کرد، که به آن‌ها اشاراتی داشت، اما هرگز به‌طور کامل بیان نمی‌شد. من این رهیافت را بسیار هیجان انگیز یافتم، آن چه که می‌گفت، در عین حال که بسیار تازه به نظر می‌رسید، اما به شکل کامل جدید و نوین نبود. ما همگی نظریه‌ی بور را از زومرفلد آموخته بودیم و موضوع را می‌دانستیم، اما شنیدن آن از دهان بور احساس کاملا متفاوتی ایجاد می‌کرد. ما به وضوح احساس می‌کردیم، او نه با انجام محاسبات پیچیده و نمایش، بلکه با نوعی شهود و الهام به نتایجش رسیده است.

هایزنبرگ، گرچه جوان بود اما از گفت‌وگو با بور و جر و بحث علیه بعضی از نکاتی که او در سخنرانی‌هایش گزارش کرده بود، تردید نداشت. یکی از این بحث‌ها به قدری جذاب بود، که استاد و شاگرد مجذوب را به بیرون گوتینگن به نزدیکی کوه هاینبرگ(Hainberg mountain) کشانید. هایزنبرگ در زندگینامه شخصی خود یادآور می‌شود؛

این پیاده‌روی، پیامدهای عمیقی در زندگی حرفه‌ای من داشت یا شاید بهتر است بگویم که، دوران کار علمی واقعی من از آن بعد ظهر به بعد آغاز شد، ناگهان آینده‌ای پر از امید و امکانات جدید در ذهنم نمایان شد، که با شکوهمندترین رنگ‌ها برای خودم تصویر می‌کردم.

 در حدود یک سال بعد هایزنبرگ به مؤسسه‌ی بور در کپنهاگ رفت و ساکنان آنجا را به‌طور حیرت انگیزی خون گرم، صمیمی و مملو از فیزیک اتمی یافت، به‌زودی احساس کرد که در خانه خودش است و به مدت چند هفته، دوباره گفت و گوهای طولانی بی نهایت آموزنده و گردش‌های پیاده‌روی با بور ادامه یافت.

نخستین پُست دانشگاهی هایزنبرگ در گوتینگن بود. در سال ۱۹۲۲، او دستیار ماکس بورن شد، متصدی قبلی این جایگاه در گوتینگن پائولی بود. بورن که تحت تاثیر استعداد شگرف پائولی قرار داشت، با دیدن هایزنبرگ خوشحالی‌اش چند برابر شد، چرا که دستیار جدید او از پائولی نیز چشمگیرتر بود. او در نامه‌ای به اینشتین نوشت:

هایزنبرگ طی زمستان با من بود، (چون زومرفلد در آمریکا بود) او بی‌تردید مانند پائولی با استعداد است، اما شخصیتی خوشایندتر دارد. او پیانو را نیز بسیار خوب می‌نوازد.

 از نظر بورن که متوجه تفاوت ورنر با پائولی بود، هایزنبرگ مانند دهقان زاده‌ی ساده‌ای، با موهای کوتاه طلایی، چشمان شفافِ شاداب و قیافه‌ای زیبا به نظر می‌رسید. هایزنبرگ دوره‌ی کاری خود در فیزیک اتمی را در زمانی بحرانی آغاز کرد،؛ هنگامی که مشکلات نظریه کوانتومی بیشتر و بیشتر مشکل آفرین می‌شد و به نظر می‌رسید که ناسازگاری‌های آن بدتر و بدتر می‌شود و ما را به سوی یک بحران می‌کشاند.

 نظریه‌ی بور(در قسمت سوم و پنجم بررسی شده است) با مسئله‌ی اتم هیدروژن معجزه کرد و همه‌ی آن چه را که می‌توانست، با نظریه اتم‌های چند الکترونی انجام داد. هایزنبرگ نخستین گام مهم را برای حل مسئله، هنگامی برداشت که با بورن به‌عنوان مربی‌اش در گوتینگن کار می‌کرد. الهام بخش هایزنبرگ، همچون اکثر موارد مهم از این نوع، یک تغییر وضعیت اجباری بود. در اواخر ماه می سال ۱۹۲۵ هایزنبرگ می‌نویسد:

من دچار تب یونجه شدم و از بورن برای مدت چهارده روز تقاضای مرخصی کردم. مستقیم عازم هلگولند(جزیره‌ی کوچکی در دریای شمال) شدم، جایی که امیدوار بودم در هوای فرح بخش دریا، دور از هرگونه گل و گیاه، به سرعت بهبود یابم. در هنگام ورود قیافه‌ی ورم کرده‌ام، باید منظره‌ای دیدنی بوده باشد. به هر حال خانم مهمانخانه دار نگاهی به قیافه من انداخت و چنین نتیجه‌گیری کرد، که باید با کسی زد و خورد کرده باشم و به من قول داد که در قبال پیامدهای بعدی از من پرستاری و مواظبت خواهد کرد. اتاق من در طبقه دوم بود و چون خانه در بلندی روی لبه‌ی جنوبی جزیره‌ی سنگی ساخته شده بود، چشم انداز باشکوهی از دهکده، تلماسه‌ها و ماورای دریا داشتم. وقتی روی بالکن نشستم، فرصت کافی داشتم تا درباره‌ی این حرف بور فکر کنم که می‌گفت به نظر می‌رسد؛ بخشی از لایتناهی در دست کسانی باشد، که به پهنه‌ی دریا می‌نگرند. به جز گردش‌های روزانه و شنا کردن‌های طولانی، چیزی نبود که توجه مرا از مسئله‌ی مورد نظرم منحرف کند و بنابراین پیشرفت من از وقتی که در گوتینگن می‌بودم سریع‌تر شد!

هایزنبرگ موفقیتش را تقریبا در زمانی به دست می‌آورد، که پائولی اصل طردش را بسط می‌داد. یادآور می‌شویم که از دید پائولی، چشم انداز اتمی را می‌توان درنهایت به‌صورت یک سیستم ریز دانه یا ریز بافتی از حالت‌های مانا دانست، که الکترون‌ها، بنابر حکم اصل طرد، اشغال کرده‌اند. نظریه‌ی پائولی گام بزرگی در تکامل مفهوم کوانتش بود. پلانک کوانتوم‌های انرژی را معرفی کرده بود؛ اینشتین نظریه‌ای از کوانتوم‌های تابش یا فوتون‌ها را مطرح کرد و بور تصویری از اتم‌ها را ساخت، که در حالت‌های مانای کوانتیده وجود دارند. پائولی وحدت این اجزای نظری را با مشخص کردن حالات مانا با اعداد کوانتومی آغاز کرد.

اما کار پائولی، خود مانند یک بنای نظری ناپیوسته بود، زیرا مجموعه چهارتایی اعداد کوانتومی که او به‌صورت اصول موضوعه گرفته بود، همان قدر بر مبنای دانش تجربی است، که بر مبنای اشتقاق نظری. نیاز مبرمی برای یک نظریه‌ی کلی وجود داشت، که اعداد کوانتومی را استنتاج کند، نه به این شکل که آن‌ها را به‌صورت اصول موضوعه در نظر بگیرد. فیزیکدانان هنوز در جست و جوی یک ترکیب عظیم بودند، که کل قلمرو کوانتومی را با آغاز از چند گزاره ریاضی در بر بگیرد.

هایزنبرگ نخستین گام‌های اطمینان بخش را در این مسیر نظری گذاشت. او اجزای اولیه نظریه‌ای را به هم متصل کرد، که سرانجام عمیقا رفتار دینامیکی اتم‌ها را می‌کاوید. این یک مکانیک اتمی ساخته شده به موازات مکانیک نیوتون، با شباهت صوری و تجریدی بود. هایزنبرگ، مانند اینشتین، اصل سازنده‌اش را در جهان ریاضیات یافت. او یک بار اظهار داشت؛ برای من طبیعی است، از دیدگاه ریاضی صوری استفاده کنم که از بعضی جهات یک داوری زیباشناختی است.

هایزنبرگ با ساده‌سازی اصول متعارف و با ساختن نظریه‌ای در امتداد خطوط ریاضی توانست، از گرفتاری‌های ناگوار نظریه‌ی بور دوری گزیند. او بدون آن که گرفتار وضع فیزیکی تک تک الکترون‌های اتمی شود، دینامیکی را ساخت که به شکل ریاضی مکانیک نیوتون بسیارشبیه بود و به‌نوعی شرح و بسط آن بود. در یک راه تجریدی مؤثر، او پلی میان جهان عادی و جهان اتمی زد. بور قبلا از این پل عبور کرده بود، اما با این تفاوت که رفتار درونی اتم‌ها را با بعضی از ویژگی‌های اشیای بزرگ مقیاس، مانند حرکت مداری سیارات، مجسم کرده بود. پُلِ هایزنبرگ به قلمرو اتمی صوری و کاملا ریاضی بود و تصویر چندان ساده‌ای از محتویات درون اتم به دست نمی‌داد.

هایزنبرگ یک سبک معماری نظری می‌ساخت، که در فیزیک اتمی ناآشنا بود. هدایت این رهیافت با مدل‌های ریاضی و از لحاظ صوری شبیه به معادلات حرکت نیوتون بود، اما از جهات دیگر تنها وابستگی مبهمی به تصویرها یا مدل‌های کلاسیک داشت. نگرش اساسی آن، که به‌زودی در نظریه‌ی کوانتومی مسلط شد و باقی ماند را بعدها پل دیراک صریحا به این صورت خلاصه کرد:

هدف اصلی علم فیزیک تهیه و تدارک تصویرها نیست، بلکه تدوین قانون‌های حاکم بر پدیده‌ها و به کار گرفتن این قانون‌ها برای کشف پدیده‌های جدید است. اگر تصویری وجود داشته باشد چه بهتر؛ اما وجود یا عدم این تصویر، تنها و تنها در درجه دوم اهمیت قرار دارد!

تحلیل هایزنبرگ دو جزء یا عامل بنیادی فیزیکی داشت، که هر دو ساده و مشاهده‌پذیر بودند، گرچه هیچ یک در پیکربندی تصویرهای فیزیکی چندان یاری نکردند. اولی مجموعه‌ی فرکانس‌های گسیل یافته از یک اتم بود، در حالتی که آن اتم بین حالت‌های مانا به شیوه‌ای که ابتدا بور پیشنهاد کرده بود، جهش می‌کند. اگر یک اتم یکی از این جهش‌های کوانتومی را از انرژی بالاتر E2 به انرژی پایین‌تر E1 انجام دهد، یک خط طیفی گسیل می‌یابد که فرکانس آن را اگر v نام‌گذاری کنیم، بنابر قاعده‌ی بور به‌صورت زیر مشخص می‌شود:

این مفهوم کلی هرفرکانس v گسیل یافته در جهش اتم بین هر دو حالت مانا با انرژی‌های Em و En را مشخص می‌کند.

این مجموعه فرکانس‌های{ vmn } تمامی خطوط مشاهده پذیر در طیف گسیلی اتم را تشکیل می‌دهد.

جز‌ء اساسی دوم تحلیل هایزنبرگ از مسئله‌ای شکل می‌گرفت، که به‌طور ضمنی در نظریه‌ی بور مطرح می‌شد، اما حل نمی شد. بور مفهوم اتم‌هایی را که میان دو حالت مانا جهش می‌کنند، به کار گرفت، اما موفق به حل این مسئله نشد که چگونه بدانیم، چه وقت و کجا اتم خاصی می‌خواهد، یک نوع جهش را انجام دهد. این مشکلی بود که رادرفورد وقتی نخستین مقالات بور را ملاحظه کرد، بلافاصله دریافت. او در سال ۱۹۱۳ به بور نوشت؛ به نظر می‌رسد شما فرض کرده‌اید، که الکترون (در حال جهش) از قبل می‌داند، کجا متوقف خواهد شد.

رادرفورد در جست و جوی یک مکانیسم جبری بود، شبیه آن چه که در فیزیک کلاسیک معمول است. بور هرگز موفق نشد، نظریه‌اش را به این کار وادار کند، اما راهنمایی ارزشمندی از مقاله‌ای را که اینشتین در سال ۱۹۱۶ نوشته بود، اخذ کرد. این ایده به ذهن اینشتین رسیده بود، که اتم‌هایی که جهش‌های کوانتومی را انجام می‌دهند، شبیه اتم‌های پرتوزای در حال فروپاشی هستند. ثابت شده است که پیش‌بینی زمان و مکان فروپاشی تک تک اتم‌ها نیز غیر ممکن است و در غیاب یک روند بهتر، قانون‌های پرتوزایی برای مدتی طولانی به‌طور آماری فرمول‌بندی می‌شده است. مثلا پیش‌بینی می‌شد، که احتمال فروپاشی اتم چقدر است. از لحاظ یک تک اتم، این یک توصیف نامعین است، زیرا گزاره‌ی آماری چیزی با قطعیت درباره فرایندهای منفرد نمی‌گوید؛ این گزاره توضیحی است، از رفتار میانگین به دست آمده از داده‌هایی که از تعداد بسیار زیادی از اتم‌ها گرفته شده است. اینشتین دریافت که این توصیف آماری را می‌توان به همه نوع تغییر اتمی بسط داد. در میان چیزهای دیگر، او ترتیبی داد، تا از یک راه فوق‌العاده ساده و کلی با تعریف احتمالات وقوع همه‌ی گذارهای اتمی ممکن، به قانون تابش پلانک برسد. بور با بهره‌گیری این موضوع را گرفت و جایی برای احتمالات گذار اینشتین در نظریه‌ی اتمی خودش یافت.

بنابراین می‌بینیم که هایزنبرگ در سال ۱۹۲۵ قانون بور-اینشتین را گسترش می‌دهد. دومین جزء سازنده‌ی فیزیکی در نسخه‌ی تحلیلی هایزنبرگ، همراه مجموعه‌ای از فرکانس‌های طیفی { vmn }، مجموعه‌ای از احتمالات گذار بود. اگر احتمال گذار m به n که با برچسب Amn نشان داده می‌شود، بزرگ باشد، احتمالا گذار صورت می‌گیرد و خط طیفی که فرکانس آن vmn است، شدید خواهد بود. پس احتمال‌های گذار تجلی شدت‌های خط طیفی مشاهده پذیرند.

هایزنبرگ دریافت که احتمال‌های گذار Amn و فرکانس‌های vmn را می‌توان در روش محاسبه‌ای به کار گرفت، که شبیه روش کاملا تثبیت شده‌ی مشهور تحلیل فوریه است. (ژوزف فوریه در اوایل قرن نوزدهم، این روش را برای نظریه‌ی تحلیلی‌اش درباره گرما، اختراع کرد) هایزنبرگ برای هر کمیت مشاهده پذیر شناخته شده در مکانیک نیوتونی یک همتای کوانتومی یافت که به‌صورت یک بسط فوریه، با فرکانس‌ها و احتمال‌های گذار، فرمول‌بندی شده بود.

در تحولات بعدی، مجموعه‌ای از احتمال‌های گذار در آرایه‌های مربعی مرتب شد، که در آن اقلام ورودی‌های مربوط‌به حالت ۱ در ردیف ۱، حالت ۲ در ردیف ۲ قرار داشتند، و غیره. اگر به‌طور کلی سه حالت دخیل باشد، آرایه‌ی مربعی به‌صورت زیر خواهد بود؛

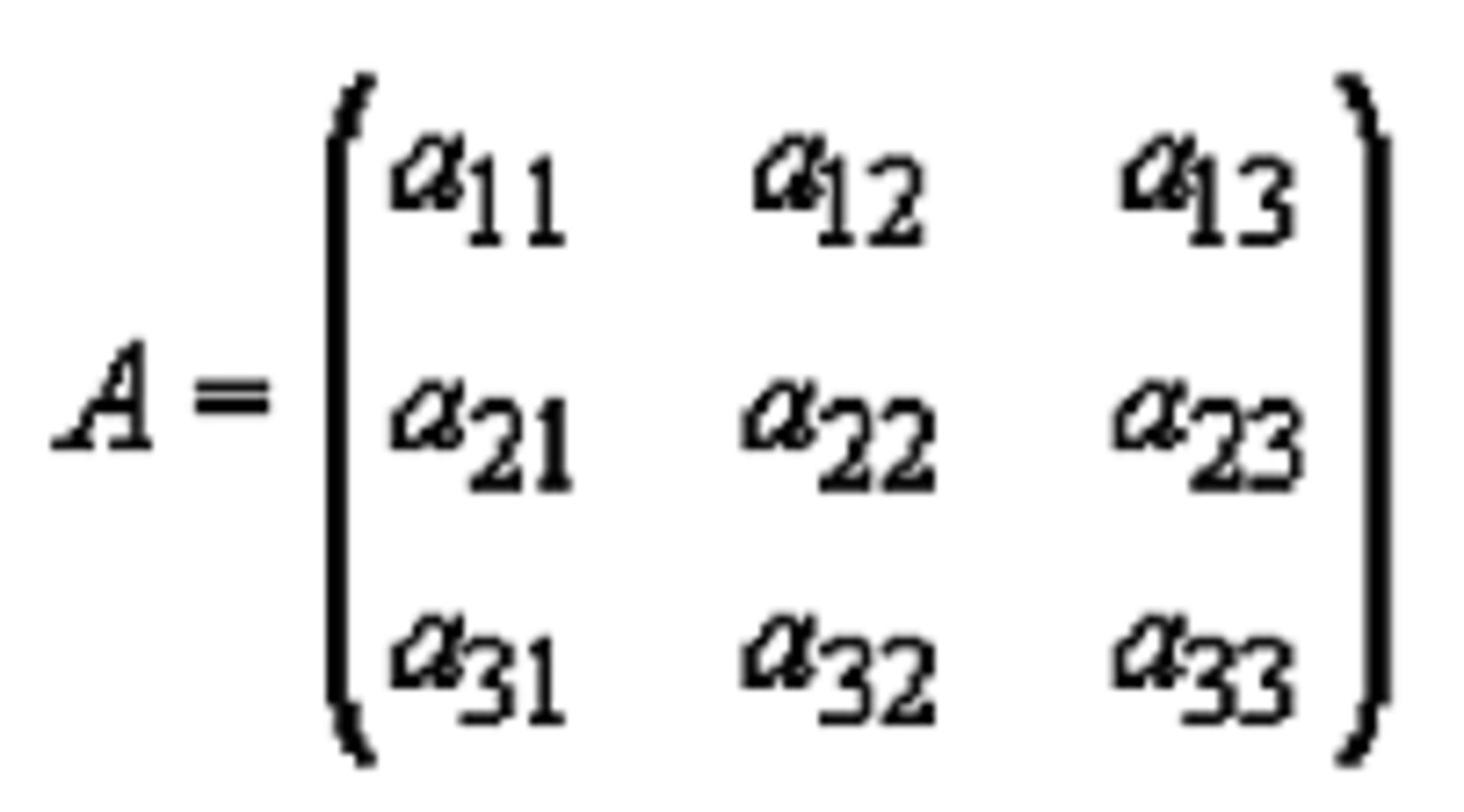
با راهنمایی روش کار فوریه، که عمدتا یک روش ریاضی بود و تلاش برای ایجاد دینامیکی که وقتی به‌جای آرایه‌ها متغیرهای متناظر کلاسیک را بگذاریم، شبیه مکانیک نیوتونی می‌شد، هایزنبرگ به یک مکانیک کوانتومی مؤثر و کارآمد رسید.

وقتی هایزنبرگ موفق شد، همه‌ی سنگ و ثقال‌های ریاضیاتی را که از گوتینگن به اتاق طبقه‌ی دوم هلگولند آورده بود، دور بریزد با دید محدودش از بی‌نهایت، به سرعت توانست شکل مکانیک جدیدش را ببیند. همچنان که مکانیک او شکل می‌گرفت، او توانست ببیند که مکانیک جدید او از لحاظ فیزیکی و ریاضی با هم سازگاری دارند، هایزنبرگ به‌شدت هیجان زده شد و با اضطراب کنجکاوانه‌ای گفت:

ابتدا نگرانی عمیقی احساس می‌کردم. احساس می‌کردم که از سطح پدیده‌های اتمی به زیبایی شگفت‌ انگیز درون آن می‌نگرم و تقریبا با این فکر دچار سرگیجه می‌شدم، که باید به تحقیق این ساختارهای غنی که طبیعت سخاوتمندانه در مقابلم گسترده است، بپردازم. نخستین محاسبات موفقیت آمیز در ساعت سه بامداد یک روز کامل شد. خواب غیرممکن بود، بنابراین، همچنان که سپیده یک روز جدید می‌دمید، عازم رأس جنوبی جزیره شدم، جایی که اشتیاق داشتم از صخره‌ای که از دریا بیرون زده بود، بالا بروم. فی‌الحال این کار را کردم و منتظر طلوع خورشید شدم.

اما هایزنبرگ به‌دنبال خوش‌بینی و هیجان اولیه‌اش، به تدریج درباره‌ی مکانیک جدیدش احساس ناراحتی می‌کرد، زیرا با نوع خاصی از جبر کار کرده بود. دو متغیر مانند x و y با روش هایزنبرگ به‌صورت آرایه‌های مربعی در می‌آمدند، که از قاعده‌ی ضرب عجیبی پیروی می‌کردند؛ حاصلضرب xy همیشه از لحاظ ریاضی، برخلاف جبر معمولی، معادل حاصل ضرب yx با عامل‌های معکوس شده نبود!

هایزنبرگ می‌نویسد:

این واقعیت که xy مساوی yx نبود، برایم ناخوشایند بود. من احساس می‌کنم که این تنها اشکال در کل طرح است؛ در غیر این صورت من کاملا خرسند بودم.

 بیشتر این نظریه در ژوئن ۱۹۲۵ ساخته شد، که هایزنبرگ یک دعوتنامه برای سخنرانی در آزمایشگاه کاوندیش در کمبریج دریافت کرد. چاره ای جز این نبود که یا کار به سرعت کامل شود یا به شعله‌های آتش سپرده شود. پائولی، این منتقد گران قدر، با خواندن دست نوشته، واکنشی شعف انگیز داشت. این اتفاق امید جدید و لذت تازه‌ای از زندگی را  به او بخشید. هایزنبرگ مقاله‌اش را به بورن ارائه کرد، اما در کمبریج از تلاش‌های اخیرش چیزی نگفت.

 بورن در ژوئیه سال ۱۹۲۵ به اینشتین نوشت:

آخرین مقاله‌ی هایزنبرگ، که به‌زودی منتشر می‌شود، تاحدی مبهم به نظر می‌رسد، اما مطمئنا درست و عمیق است.

 برای بورن، آشکار بود که یک مکانیک کوانتومی واقعی در دسترس است و او بسط و توسعه‌ی یک گزاره‌ی ریاضی کامل از این نظریه را آغاز کرد. او به‌ویژه درباره‌ی قاعده‌ی ضرب چشمگیری کنجکاو شد؛

قاعده‌ی ضرب نمادین هایزنبرگ مرا آرام نمی‌گذاشت و پس از روزها تفکر متمرکز و آزمودن، نظریه‌ی جبری را به یاد آوردم که از معلمم، روزانس، در برسلاو آموخته بودم.

این نظریه‌ی جبری مربوط‌به ماتریس‌ها بود، موجودات ریاضیاتی آرایه‌گونه که جبر آن را آرتور کیلی، با بصیرت یک ریاضیدان، در حدود هفتاد سال پیش فرمولبندی کرده بود، قاعده‌ی ضرب عجیبی که هایزنبرگ کشف کرد، دقیقا مشابه ضرب ماتریسی بود؛ هایزنبرگ آرایه‌ها را رسما به شکل ماتریس‌ها در نظر گرفت. وقتی بورن این سرنخ را به دست آورد، راه برای بسط و توسعه یک مکانیک ماتریسی کوانتومی گشوده شد. این کار به وسیله‌ی بورن، هایزنبرگ و یک متخصص جوان ماتریس، به نام پاسکوال جردن آغاز شد.

بورن و هایزنبرگ خودشان را در جهان ریاضیاتی بیگانه‌ای می‌یافتند، که به زبان آن چندان آشنا نبودند. هایزنبرگ به جردن گلایه می‌کرد که؛ حتی نمی‌دانم ماتریس چیست!

اما از قضا فیزیکدانان گوتینگن از لحاظ توصیه‌ی مفید درباره‌ی چگونگی برخورد با مشکلات ریاضیاتشان کمبودی نداشتند. ریاضیدان بزرگ دیوید هیلبرت که در گوتینگن بود، بهتر از هر کسی در جهان، ضرورت یادگیری زبان ریاضی مورد نیاز فیزیکدانان را بیان می‌کرد. ادوارد کاندن، یک آمریکایی که در گوتینگن بود، درباره توصیه هیلبرت می‌گوید:

هیلبرت به بورن، هایزنبرگ و فیزیکدانان نظری گوتینگن می‌خندید، زیرا وقتی آنان نخستین بار مکانیک ماتریسی را کشف کردند، زحمت زیادی را متحمل شدند، اما هرکس دیگری هم که می‌کوشید مسئله‌ای را با ماتریس حل کند، یا واقعا ماتریس‌ها را به کار گیرد و با آن‌ها کار کند، همان زحمت را داشت. بنابراین آنان از هیلبرت کمک خواستند.

هیلبرت به آنان گفت، که ماتریس‌ها برای او ابزارهایی ساده و مفید برای توضیح بعضی از جنبه‌های رسمی مسائلی هستند، که به زبان دیگر، یعنی با معادلات دیفرانسیلی نوشته شده‌اند. چون فیزیکدانان سال‌های متمادی از زبان معادلات دیفرانسیل برای مسائل دیگری استفاده کرده بودند، هیلبرت پیشنهاد کرد که ماتریس‌ها ممکن است، جلوه‌هایی از معادلات مفیدتر از نوع دیفرانسیلی باشند. بنابر نظر کاندن، نظریه پردازان گوتینگن این حرف را، ایده‌ی احمقانه‌ای می پنداشتند، که هیلبرت خودش نمی‌دانست درباره‌ی چه چیزی حرف می‌زند، اما هیلبرت به ندرت اشتباه می‌کرد.

درست شش ماه بعد، اروین شرودینگر به معادلاتی که هیلبرت پیش‌بینی کرده بود، دست یافت و ثابت کرد که آن‌ها با همان روش‌های معمول معادلات دیفرانسیل، همان کار و بیشتر از آن را به انجام می‌رسانند!

همان‌طور که در ابتدا اشاره کردیم، هایزنبرگ زندگینامه و مباحث خود را در کتابی به قلم تحریر در آورده است، در اینجا به مطالعه‌ی مباحثه‌ی او با اینشتین پیرو یک سلسله مباحث بنیادی می‌پردازیم.

سیر فیزیک اتمی در آن سال‌های حسّاس آنچنان بود، که نیلس بور هنگام گردش با من در تپّه‌های هاینبرگ پیشبینی کرده بود. دشواری‌ها و تناقضات درونی‌ای که بر سر راه فهم از اتم و پایداری آن قرار داشت، نتوانست اندکی کاهش یابد، یا برطرف شود. به عکس این دشواری‌ها هر روز با شدّت بیشتری نمودار می‌شد. هر کوششی که انجام می‌شد، تا بر این دشوار‌ی‌ها با ابزارهای مفهومی‌ که پیش‌تر در فیزیک وجود داشت، چیره شویم، چنین می‌کرد که از همان آغاز به شکست حتمی می‌انجامد.

از این‌گونه می‌توان به کشف دانشمند آمریکایی کامپتون، که براساس آن نور (یا اگر بهتر بگوییم: پرتو رونتگن) به هنگام پراکندگی الکترونی عدد ارتعاشش تغییر می‌کند، اشاره کرد. در این آزمایش، اگر چنین فرض می‌کردیم که نور، آنچنان که اینشتین پیشنهاد کرده بود، از ذرات کوچکی یا از بسته‌های انرژی درست شده است، که با سرعت زیاد در فضا حرکت می‌کند و گاهی، حتّی به سبب فرایند پراکندگی، با الکترونی برخورد می‌کند، این نتیجه را می‌توانستیم توضیح دهیم. اما از سوی دیگر آزمایش‌های زیادی هم نشان می‌دهد، که نور با امواج رادیویی اساسا فرقی ندارد، مگر به سبب طول موج کوتاه‌تر؛ این سخن بدین معنی است که، پرتو نوری درعین حال فرایندی موجی است و نه جریانی از ذرات و شگفت‌تر از این آن نتایج اندازه‌گیری‌هایی بود، که فیزیکدان هلندی اورناشتاین به دست آورده بود. در اینجا حرف از این بود تا نسبت شدت خطوط طیفی را معین کنیم، که در آن به اصطلاح گروه خطوط طیفی جمع شده است. این نسبت‌ها را می‌توانستیم با نظریه‌ی بور پیش‌بینی کنیم. آنچه عاید شد این بود که، هرچند صورت‌بندی‌هایی که از نظریه‌ی بور به دست آمده است، درآغاز نادرست است، اما بااندکی تغییر در این روابط به فرمول‌هایی می‌توانستیم برسیم، که به‌طور آشکار با تجربه درست‌تر مطابقت داشت و این چنین شد که آموختیم، تا با دشواری‌ها اندک اندک کنار بیاییم و به این کار هم عادت کردیم، تا مفاهیم و تصوراتی را که از فیزیک پیش‌تر در حوزه‌ی اتم وارد کرده بودیم هم نیمه درست بدانیم و هم نیمه نادرست و بر کاربرد آن‌ها هم معیارهای سفت و سختی نباید قرار دهیم و از طرفی هم با استفاده از تیزهوشی توانستیم گاه صورت‌بندی‌های درست این جزییات را به‌سادگی به گمان دریابیم. 

در درس‌های گروهی‌ای که زیر نظر ماکس بورن، در نیمسال تابستانی ۱۹۲۴ در گوتینگن برقرار شد، دیگر حرف از مکانیک کوانتومی تازه‌ای بود، که روزی باید به‌جای مکانیک نیوتونی دیرین بنشیند، که در آن زمان تنها در جاهایی جزییات منفردی از آن چارچوب را می‌توانستیم دریابیم و حتی در نیمسال زمستانی بعد، که من دوباره موقتا در کپنهاگ کار می‌کردم و می‌کوشیدم تا نظریه‌ای را گسترش دهم، که کرامرز درباره‌‌ی پدیده‌هایی، که آن‌ها را پدیده‌های پاشیدگی می‌نامیدیم، مطرح کرده بود، همه‌ی فکر ما بر این کار متمرکز بود تا نه اینکه همه‌ی روابط ریاضی درست را بدست آوریم، بلکه آن‌ها را به سبب شباهت‌هایی که با فرمول‌های نظریه‌ی کلاسیک داشت، به گمان دریابیم.

هنگامی که به وضع نظریه‌ی اتمی در آن ماه‌ها فکر می‌کنم، همواره به یاد گردشی می‌افتم، که شاید در اواخر پاییز سال ۱۹۲۴ با برخی از دوستانم در جنبش جوانان، در کوه‌های میان کرویت و دریاچه‌ی آخن رفته بودیم. هوای درّه در آن روز گرفته بود و ابرها هم کوه‌ها را در پرده‌ی خود کاملا پوشانده بود. با بالارفتن از کوه ابرها راه را بیشتر و بیشتر بر ما تنگ‌تر می‌کرد، به طوری که پس از ساعتی خود را هرچه بیشتر در میان کلاف سردرگمی از صخره‌ها و رستنی‌ها یافتیم، که در آن دیگر یافتن راه از چاه، هرچقدر هم که می‌کوشیدیم، ممکن نبود. اما ما هم به بالارفتن ادامه می‌دادیم، شاید هم با این دلهره که آیا اصلا می‌توانیم، در صورتی که حادثه‌ای بروز کند راه برگشت را بازهم پیدا کنیم. اما همچنان که بالا می‌رفتیم، تغییری شگفت پدیدار شد. مه در جاهایی آن چنان غلیظ بود که ما دیگر یکدیگر را نمی‌دیدیم و تنها با داد زدن می‌توانستیم، چیزی به همدیگر بگوییم. اما ناگهان بالای سرمان روشن‌تر شد، روشنایی هم به یکباره تغییر کرد. پیدا بود که ما در میدانی از مه وارد شده بودیم، که از بالای سرمان رد می‌شد و یک دفعه هم توانستیم از میان دو توده‌ی غلیظ لبه‌ی روشن دیواره‌ی صخره‌ای بلند را ببینیم، که در میان نور خورشید پدیدار شده بود، که از روی نقشه‌ی راه در پی‌اش بودیم. چند نگاهی به این طرف و آن طرف کافی بود، تا به تصویری روشن از آن چشم‌انداز کوهستانی برسیم، که شاید پیش روی ما و بالای سرما بود و پس از آن که ده دقیقه‌ی دیگر بازهم از سربالایی تندی بالا رفتیم، به گردنه‌ای رسیدیم که بر فراز آن دریای مه بود و خورشید در آن پیدا. در جنوب، ستیغ کوه‌های زون‌وند و در پشت آن قله‌های پوشیده از برف آلپ مرکزی با وضوح هرچه تمام‌تر دیده می‌شد، به طوری که دیگر جایی برای دودلی بر بالارفتن باقی نمی‌گذاشت.

در فیزیک اتمی هم در زمستان ‍۱۹۲۴/۱۹۲۵ شاید در چنین حوزه‌ای وارد شده بودیم، که در آن مه هم، گاه چشم چشم را نمی‌دید، اما شاید بتوان گفت، که بالای سرمان هوا روشن‌تر می‌کرد. آن گرگ و میش هوا، نوید از چشم‌اندازی تازه می‌داد که، برایمان بسیار اهمیت داشت.

دانشگاه برلین در آن زمان کانون فیزیک در آلمان بود .افرادی چون پلانک، اینشتین، فون لاوئه، و نرنست در آنجا بودند. پلانک نظریه‌ی کوانتومی را در همین‌جا کشف کرده بود و روبنس آن را با اندازه گیری‌های خودش از تابش گرمایی تأیید کرده بود، اینشتین هم در سال ۱۹۱۶ نظریه‌ی نسبیت عام و نظریه‌ی گرانش خود را صورت‌بندی کرده بود. مرکز زندگی علمی، آن گردهمایی فیزیک بود که به سنتی از زمان هلمهولتس باز می‌گشت و در آن به‌خصوص استادان فیزیک پرشمار بودند. در آغاز سال ۱۹۲۶ از من دعوت شد، تا درچارچوب این گردهمایی درباره‌ی نظریه‌ی تازه پیداشده‌ی مکانیک کوانتومی گزارش دهم. اما چون این نخستین باری بود، که با این صاحب‌نامان پرآوازه آشنا می‌شدم، زحمت زیادی بر خود هموار کردم، تا آن مفاهیم را که برای فیزیک آن زمان نامأنوس بود و بنیان ریاضی آن نظریه‌ی تازه را تا حد ممکن، به روشنی نشان دهم، به طوری که توانستم به‌خصوص دلبستگی اینشتین را برانگیزم. پس از پایان گردهمایی اینشتین از من درخواست کرد تا او را تا خانه‌اش همراهی کنم، تا آنجا بتوانیم درباره‌ی افکار تازه به تفصیل بحث کنیم. 

 در راه خانه، اینشتین درباره‌ی سیر تحصیلاتم و از دلبستگی‌های امروزیم در فیزیک پرسید. همین که وارد خانه شدیم، گفت‌وگو را فورا با پرسشی شروع کرد که به پیش شرط‌های فلسفی کار من مستقیما برمی‌گشت؛

این چیزهایی که آنجا برای ما تعریف کردید، به نظرم بسیار عجیب آمد. شما قبول دارید که الکترون در داخل اتم وجود دارد و به یقین هم حرف شما درست است؛ اما می‌خواهید مسیر الکترون در اتم را از ریشه باطل کنید، هرچندکه ما مسیر الکترون را در اتاقک ابر می‌توانیم مستقیم ببینیم، ممکن است دلایل این فرض عجیب را کمی دقیق‌تر توضیح دهید. 

من هم این‌گونه جواب دادم؛

مسیر الکترون در اتم را نمی‌توانیم ببینیم، اما از تابشی که از اتمی از راه فرایند تخلیه گسیل می‌شود، می‌توانیم بازهم مستقیما بسامد ارتعاش را و دامنه‌ی وابسته به آن را، نتیجه بگیریم. پس شناخت ما از کل عدد ارتعاش و دامنه در فیزیک حتی تا امروز هم، مثل جایگزینی است بر شناخت ما از مسیر الکترون، اما چون منطقی هم هست تا در هر نظریه‌ای تنها آن کمیت‌هایی را بپذیریم، که می‌تواند مشاهده شود، به نظرم درست آمد تا تنها این کُل را، مثلا به‌عنوان نماینده‌ی مسیر الکترون بدانیم.

اینشتین در جوابم گفت:

ببینم، شما که جدی نمی‌گویید، که در نظریه‌ فیزیکی تنها باید کمیت‌های مشاهده‌پذیر را به حساب آورد.

باتعجّب پرسیدم؛

فکر می‌کردم، که اصلا این خود شما بودید که این فکر را اساس نظریه‌ی نسبیت کرده‌اید؟ شما خودتان تاکید دارید، که اصلا نباید از زمان مطلق حرف زد، چرا که زمان مطلق را نمی‌توان مشاهده کرد. فقط اخبار ساعت‌ها، چه در نظام مرجع ساکن باشد و چه متحرک، در تعیین زمان ملاک است.

اینشتین جواب داد:

شاید من از چنین فلسفه‌ای استفاده کرده باشم، اما این هم بی‌معنی است. یا می‌توانم بااحتیاط بیشتری بگویم، که شاید این ارزش راهنمای جست‌وجو را داشته باشد، تا آن چیزی را به یاد آوریم که درواقع مشاهده کرده‌ایم. اما از نظر اصولی کاملا نادرست است، که بخواهیم نظریه‌ای را تنها براساس کمیت‌هایی بنا کنیم که مشاهده‌پذیر باشد، زیرا که درواقع قضیه کاملا بالعکس است. این نظریه است که از همان اول حکم می‌کند، که چه چیزی را می‌توان دید. ببینید، مشاهده اصلا فرایند پیچیده‌ای است. آن فرایندی که باید مشاهده شود، برخی رویدادها را در دستگاه اندازه‌گیری ما فرا می‌خواند. درنتیجه، در دستگاه فرایندهای دیگری جریان پیدا می‌کند، که سرانجام از بیراهه‌هایی تاثّر حسی و تثبیت نتیجه را در آگاهی ما برمی‌انگیزد. در سراسر این راه دراز، از پدیده گرفته تا تثبیت آن در آگاهی ما، باید بدانیم که طبیعت چگونه کار می‌کند، باید قوانین طبیعت را دست کم به‌طور عملی بشناسیم، اگر اصلا بخواهیم ادعا کنیم که چیزی را مشاهده کرده‌ایم، تنها نظریه، یعنی شناخت قوانین طبیعت، به ما این امکان را می‌تواند بدهد، تا بتوانیم از تاثّر حسی به آن پدیده‌ای که در بنیان آن قرار دارد، برسیم. اگر ادعا کنیم که چیزی را می‌توانیم مشاهده کنیم، پس باید هم درواقع این طور دقیق‌تر بگوییم؛ هرچند که خود را آماده می‌کنیم تا قوانین طبیعی تازه‌ای را صورت‌بندی کنیم، که با قوانین پیشین مطابقت ندارد، اما بازهم چنین گمان می‌کنیم که قوانین طبیعی موجود، در راهی که قرار دارد، از پدیده‌ای که موضوع مشاهده است تا زمانی‌که به آگاهی ما می‌رسد، آنچنان درست عمل می‌کند که می‌توانیم به آن‌ها اعتماد کنیم و درست به همین سبب است، که می‌توانیم از مشاهده سخن بگوییم. برای مثال در نظریه‌ی نسبیت، پیشفرض این است که حتی در چارچوب نظام متحرک، پرتوهای نور، که از ساعت به چشم مشاهده‌گر می‌رسد، آن قدر درست عمل می‌کند، که پیش‌تر از آن‌ها انتظار داشتیم و شما هم با نظریه‌تان آشکارا چنین فرض می‌کنید که همه‌ی آن سازوکار تابش نور، از اتم درحال ارتعاش گرفته تا طیف‌نما یا تا چشم، درست همان‌طور کار می‌کند، که همواره فرضمان بوده است، یعنی در اساس طبق قوانین ماکسول؛ اگر وضع به این صورت نباشد، پس آن کمیت‌هایی را که شما مشاهده‌پذیر می‌دانید، اصلا نمی‌توانید مشاهده کنید. ادعای شما مبنی بر اینکه تنها کمیت‌های مشاهده‌پذیر را وارد می‌کنید، درواقع هم گمانی است درباره‌ی یکی از خصوصیات نظریه‌ی شما، که شما هم بر صورت‌بندی آن می‌کوشید. شما خیال می‌کنید، که نظریه‌تان آن تشریحی را که تاکنون از فرایند تابش داشتیم، در آن نقاطی که شما به آن‌ها در اینجا اشاره می‌کنید، دست نخورده برجا می‌گذارد. شاید شما درست می‌گویید، اما این نکته به هیچ وجه مسلم نیست!

نظر اینشتین برایم بسیار دور از انتظار بود، هرچندکه دلایلش روشنگر بود و به همین سبب هم در جواب، از او سؤال کردم:

این فکر که یک نظریه درواقع جمع بندی است‌ از مشاهدات ذیل، اصل صرفه‌جویی در فکر است، که در حقیقت برگرفته از نظرات ماخ، فیزیک‌دان و فیلسوف، است و بازهم ادعا شده است، که خود شما در نظریه‌ی نسبیت از این فکر ماخ استفاده‌ی زیادی کرده‌اید. اما با آنچه اکنون گفتید به نظرم می‌رسد که شما درست در جهت عکس می‌روید. پس من دقیقا باید کدام حرف را قبول کنم، یا بهتر بگویم، اصلا نظر شما در این‌باره چیست؟

و اینشتین چنین پاسخ داد:

این داستان مفصلی است، اما حالا دیگر به تفصیل از آن حرف می‌زنیم. این مفهوم صرفه‌جویی در فکر بخشی از حقیقت را دارد، اما به نظرم خیلی پیش پا افتاده می‌آید. من در ابتدا دو دلیل به سود ماخ می‌آورم. رفتار ما با دنیا آشکارا فراتر از حواس ما می‌رود. وقتی ما چون بچه‌های کوچک حرف زدن و فکر کردن را یاد می‌گیریم، اتفاقی که می‌افتد این است، که ما این امکان را می‌‍‌‌‌شناسیم تا مفاهیم بسیار پیچده را، آن تاثرات حسی را که به نحوی به هم مرتبط است، با یک کلمه نشان دهیم، مثلا با کلمه‌ی توپ! ما این را از بزرگ‌ترها یاد می‌گیریم و از اینکه می‌توانیم منظورمان را به آن‌ها بفهمانیم، دلشادیم. پس می‌توانیم هم بگوییم که ساخت کلمه و به همراه آن مفهوم توپ عمل صرفه‌جویی فکری است، زیرا که این صرفه‌جویی این امکان را می‌دهد، تا تاثرات حسی کاملا پیچیده را به‌سادگی باهم جمع کنیم و هیچکس هم سراغ این پرسش نمی‌رود که چه شرایط جسمی و فکری در انسان (دراینجا  مراد نزد کودک است) باید موجود باشد، تا این فرایند فهمیدن آغاز شود و تا آنجا هم که می‌دانیم، این فرایند نزد حیوانات بسیار کم ثمرتر است، اما فعلا با آن کاری نداریم. ماخ حرفش را این‌گونه ادامه می‌دهد، که ساخت نظریه‌های علمی و شاید نظریه‌های بسیار پیچیده اساسا به شیوه‌ای مشابه محقق می‌شود، یعنی می‌کوشیم تا پدیده‌ها را به‌صورت واحد مرتب کنیم، آن‌ها را به طریقی به شکلی ساده برگردانیم، تا اینکه شاید به کمک مفاهیم کمتری بتوانیم دسته‌ای از رویدادها را که محتوای بیشتری دارد فهم کنیم و این فهمیدن چیزی جز آن نیست، تا این رویدادها را با این مفاهیم ساده در کثرت خود دریابیم. همه‌ی اینها کاملا پذیرفتنی است، اما بازهم باید از خود پرسید که اصلا منظور ما از این اصل صرفه‌جویی در فکر چیست! آیا اصلا حرف از صرفه‌جویی روانی است یا منطقی، یا اصلا طور دیگری بپرسیم، که آیا حرف از وجه عینی رویداد است، یا وجه ذهنی آن. وقتی کودک مفهوم توپ را درست می‌کند، آیا با این کار به ساده سازی‌ای ذهنی دست می‌یابد، زیراکه تاثرات حسی پیچیده با این مفهوم توپ باهم جمع می‌شود، یا آنکه توپ درواقع وجود دارد؟ جواب ماخ؛ شاید این باشد که گزاره‌ی توپ درواقع وجود دارد، اصلا محتوایی بیش از حکم تاثرات حسی ندارد، که دراین جا به‌سادگی باهم جمع شدنی است، اما این جا دیگر ماخ اشتباه می‌کند، زیرا اول آن که گزاره‌ی توپ درواقع وجود دارد، مجموعه‌ای از اخباری درباره‌ی تاثرات حسی ممکن را دربردارد، که شاید در آینده پدیدار شود. ممکن، یعنی آنچه انتظار وقوعش را داریم، بخش مهمی از واقعیت ماست، که این بخش نباید درکنار امر واقع به‌سادگی فراموش شود و دوم اینکه باید به این نکته هم فکر کنیم، که نتیجه‌گیری از تاثرات حسی از تصورات و چیزها از پیش شرط‌های بنیادی فکر ماست و بنابراین اگر بخواهیم تنها از تاثرات حسی حرف بزنیم، باید زبان و فکر را هم از خود سلب کنیم. به عبارت دیگر، این واقعیت که جهان به واقع وجود دارد، که در پس تاثرات حسی ما چیزی عینی وجود دارد، نزد ماخ دچار کاستی است. من هم اصلا نمی‌خواهم در اینجا حرفم از واقع‌گرایی بی‌آلایش باشد؛ من خوب می‌دانم که در اینجا حرف از پرسشی دشوار درمیان است، اما مفهوم ماخ از مشاهده هم خیلی ساده انگارانه است. ماخ طوری رفتار می‌کند، گویی که می‌دانیم معنای واژه‌ی مشاهده چیست و چون عقیده دارد که در این جایگاه می‌تواند به تصمیمی درباره‌ی عینی و ذهنی برسد، مفهومش از سادگی خصلتی مظنون به بازاری بودن به خود می‌گیرد، یعنی همان صرفه‌جویی در فکر! این مفهوم رنگی کاملا ذهنی دارد، در واقعیت، این سادگی قوانین طبیعت یک امر واقع عینی است و این هم وابسته به این است که در مفهوم سازی درست، وجه عینی و وجه ذهنی سادگی را در توازنی درست با یکدیگر بگذاریم و این همان چیزی است که خیلی مشکل است. ولی اکنون بهتر است دوباره به موضوع سخنرانی شما برگردیم. گمان من این است، که شما درست از همان جایی که درباره‌اش حرف زدیم، بعدها در نظریه‌تان دشواری‌هایی پیدا خواهید کرد. من هم می‌خواهم دراین مورد دلایل بهتری بیاورم، شما طوری رفتار می‌کنید مثل اینکه همه چیز را می‌توان در وجه مشاهده به همان حال سابقش باقی گذاشت، یعنی مثل اینکه شما می‌توانید به‌سادگی به زبان معمول آن چیزی را بگویید، که فیزیکدان مشاهده می‌کند. پس باید هم بتوانید بگویید؛ ما در اتاقک ابر مسیر الکترون را از راه اتاقک می‌بینیم. اما به نظر شما در اتم، مسیر الکترون وجود ندارد. مسلم است، که این حرف آشکارا بی‌معنی است. چون با کوچک‌تر کردن فضایی که الکترون در آن حرکت می‌کند، نمی‌توان مفهوم مسیر را هم از اعتبار ساقط کرد.

اکنون نوبت من شده بود، تا بار دیگر از مکانیک کوانتومی تازه دفاع کنم؛

در حال حاضر، ما اصلا نمی‌دانیم که به چه زبانی می‌توانیم از آنچه در اتم می‌گذرد، حرف بزنیم. این هم درست است، که ما زبانی ریاضی، یعنی گرته‌ی ریاضی‌ای در اختیار داریم که به کمک آن می‌توانیم، حالات مانای اتم یا احتمال گذار از مرحله‌ای به مرحله دیگر را محاسبه کنیم. اما دست کم هنوز هم به‌طور کلی نمی‌دانیم که این زبان با زبان معمول چه رابطه‌ای دارد. مسلم است که به این رابطه نیاز داریم تا اصلا بتوانیم نظریه را در آزمایش‌های خود به کار گیریم؛ چون درباره‌ی آزمایش‌ها هنوز هم با زبان معمول حرف می‌زنیم، یعنی به زبان معمول در فیزیک کلاسیک!من هم نمی‌توانم ادعا کنم، که ما هم تا حالا مکانیک کوانتومی را فهیمده‌ایم. گمان می‌کنم که آن گرته‌ی ریاضی چیز درستی است، اما ارتباط آن با زبان معمول هنوز برقرار نشده است. زمانی در این راه کامیاب شویم، در آن روز می‌توانیم امیدوار باشیم که درباره‌ی مسیر الکترون در اتاقک ابر هم آن‌گونه حرف بزنیم که هیچ تناقض درونی در آن پدیدار نشود. شاید هنوز خیلی زود باشد تا این مشکلات حل شده باشد!

اینشتین گفت:

بسیار خوب، این درست. در سال‌های آینده بازهم فرصتی پیش می‌آید، تا بازهم با یکدیگر در این‌باره حرف بزنیم. اما شاید لازم باشد تا درباره‌ی سخنرانی شما سؤال دیگری مطرح کنم. این مکانیک کوانتومی شما دو وجه متفاوت دارد؛ از یک طرف این مکانیک کوانتومی، آن چنان که به‌خصوص بور هم به درستی بر آن تاکید داشت، به پایداری اتم می‌پردازد؛ یعنی می‌گذارد تا صورت‌های تازه‌ای پدیدار شود. اما از طرفی هم عنصر غریب ناپیوستگی را، بی‌ثباتی در طبیعت را تشریح می‌کند، که ما آن را برای مثال درست به عینه می‌بینیم، وقتی که در تاریکی بر پرده‌ای فلوئورسان درخشش‌هایی را می‌بینیم، که از ترکیبی از مواد پرتوزا بیرون می‌رود. این دو وجه مسلما به یکدیگر مرتبط است. در مکانیک کوانتومی شما، شما هم باید از هردو وجه حرف بزنید، مثلا اگر بخواهید از گسیل نور از اتم حرف بزنید. شما می‌توانید مقادیر گسسته‌ی انرژی در حالات مانا را محاسبه کنید. نظریه‌ی شما به نظر می‌رسد که باز هم می‌تواند به حساب پایداری برخی از صورت‌ها رسیدگی کند، که نمی‌تواند پیوسته از یکی به دیگری گذر کند، بلکه درست در مقادیر پایان‌داری باهم اختلاف دارد و پیوسته هم آشکارا دوباره از نو درست می‌شود. اما بر سر گسیل نور چه می‌آید؟ شما می‌دانید که پیشنهاد من این بود که اتم از مقدار انرژی مانایی به مقدار دیگر ناگهان فرو می‌افتد، به طوری که این اختلاف انرژی را، مانند بسته‌ای از انرژی، یعنی همان کوانتوم نور، گسیل می‌کند. این خودش به‌خصوص نمونه آشکاری از آن عنصر بی ثباتی است. آیا به عقیده شما این تصور درست است؟ آیا شما هم می‌توانید گذار از حالت مانایی را به حالت دیگر به طریقی دقیق‌تر تشریح کنید؟

در جوابم ناچار شدم به حرف بور برگردم؛

گمان می‌کنم از بور آموخته باشم، که از چنین گذاری در مفاهیم کنونی اصلا نمی‌توان حرفی در میان باشد و اصلا این گذار را نمی‌توان چون فرایندی در زمان و مکان تشریح کرد. با این حرف هم البته چیز زیادی عاید نمی‌شود، یعنی فقط این را می‌گوییم، که اصلا در این‌باره چیزی نمی‌دانیم و دراین مورد هم که من کوانتوم‌های نور را قبول دارم یا نه، اصلا نمی‌توانم تصمیمی بگیرم. تابش آشکارا همان عنصر بی‌ثباتی را دارد، که خود شما آن را با کوانتوم‌های نور نشان می‌دهید. اما از طرفی هم تابش عنصر روشن پیوستگی را دارد، که در پدیده‌های تداخل پدیدار می‌شود و آن را با نظریه‌ی موجی نور به ساده‌ترین صورتی می‌توان تشریح کرد. اما شما هم البته به حق می‌پرسید، که آیا با این مکانیک کوانتومی تازه، که آن را هم درواقع هنوز نفهمیده‌ایم، می‌توان چیزی درباره این پرسش‌های ترسناک بسیار دشوار آموخت. گمان می‌کنم، که به چنین چیزی می‌توانیم امید داشته باشیم. می‌توانم تصور کنم که اگر مثلا به اتمی بنگریم، که به تبادل انرژی با اتم‌های دیگر در محیط یا با میدان تابش می‌پردازد، اخبار خوبی از آن به دست آوریم. در این حالت است که شاید بتوان درباره تغییرات انرژی در اتم چیزی پرسید. وقتی انرژی از روی بی‌ثباتی تغییر می‌کند، همان‌طور که خود شما از تصورتان از کوانتوم‌های نوری انتظار دارید، در این صورت آن تغییرات، یا اگر بخواهیم به زبان ریاضی آن را درست‌تر بیان کنیم، یعنی آن تغییرات میانگین مربع بزرگ‌تر از حالتی خواهد بود، که انرژی پیوسته تغییر می‌کند. نظر خود من این است که از مکانیک کوانتومی آن مقدار بزرگ‌تر به دست می‌آید، به طوری که می‌توان آن عنصر بی ثباتی را مستقیم دید. اما از طرفی هم باید بتوان آن عنصر پایداری را شناخت، که در آزمایش تداخل پدیدار می‌شود. شاید ناگزیر باشیم تا گذار از حالت مانایی به حالت دیگری را شبیه آن چیزی تصور کنیم، که در فیلم‌ها به‌صورت گذار از یک تصویر به تصویر بعدی است. این گذار ناگهانی نیست، بلکه تصویری کم کم ضعیف‌تر می‌شود، تا تصویر دیگر به آرامی روشن‌تر شود، به طوری که برای مدتی هردو تصویر درهم می‌رود و کسی هم نمی‌داند که اصلا منظور از این کار چه بوده است. شاید در اتم‌ها هم حالتی میانی وجود داشته باشد، که در آن حالت نمی دانیم که آیا اتم در حالت بالایی است یا در حالت پایینی!

اینشتین با هشدار به من گفت:

افکار شما به سمت بسیار خطرناکی در حرکت است. شما به یک‌باره از آن چیزی حرف می‌زنید که درباره‌ی طبیعت می‌دانیم و نه از آن چیزی که خود طبیعت درواقع انجام می‌دهد، در علم فقط می‌تواند حرف از این باشد تا آن چیزی را بیرون بکشیم که طبیعت درواقع انجام می‌دهد. شاید هم کاملا محتمل باشد که آنچه من و شما اصلا از طبیعت می‌دانیم، با هم فرق داشته باشد. اما به این موضوع اصلا چه کسی دلبسته است؟ شاید فقط من و شما و دیگران هم شاید اصلا به آن بی اعتنا باشند. اگر نظریه‌ی شما درست باشد، پس باید روزی هم برگردید و به من بگویید که اتم چه کار می‌کند، وقتی از حالت مانایی از راه گسیل تابش به حالت دیگری می‌رود؟

با دودلی و شک این طور جواب دادم:

 به نظرم می‌رسد که شما در استفاده از زبان کمی بیش از حد سخت‌گیری می‌کنید. اما این را هم قبول دارم که هرچه حالا بگویم، بهانه‌ای بیش نیست. پس صبر می‌کنیم تا ببینیم که نظریه‌ی اتمی چگونه پیش خواهد رفت.

اینشتین چپ چپ نگاهی به من انداخت و چنین گفت:

چرا این قدر به نظریه‌تان محکم یقین دارید، درحالی‌که این همه مسائل مهم، هنوز کاملا بی‌پاسخ مانده است؟

به یقین هم مدتی طول کشید، تا توانستم به پرسش اینشتین جواب بدهم. اما بعد هم شاید چیزی دراین حدود گفتم:

من هم درست مثل شما عقیده دارم، که سادگی قوانین طبیعت خصلتی عینی دارد و فقط هم حرف از صرفه‌جویی در فکر نیست. وقتی طبیعت ما را به سوی صورت‌های ریاضی، که سادگی و زیبایی بسیار دارد، راهنمایی می‌کند و با صورت هم منظورم اینجا این است؛ نظام‌های کامل از فرضیه‌ها، اصول موضوعه و امثال آن‌ها که پیش‌تر کسی به آن‌ها نیندیشیده بود، پس نباید هم جز این گمان کنیم، که این صورت‌ها حقیقی است، یعنی آن که خصوصیتی اصیل از طبیعت است. شاید هم این صورت‌ها به رابطه‌ی ما با طبیعت هم بپردازد، یعنی عنصری از صرفه‌جویی در فکر را هم داشته باشد. اما از آن جایی که ما هم به خودی خود هرگز به این صورت‌ها نمی‌رسیدیم، از آن جایی که طبیعت آن‌ها را به ما نشان داده است، پس این صورت‌ها تنها از آنِ افکار ما درباره واقعیت نیست و از آنِ واقعیت نیز هست!شما هم شاید به من معترض باشید که، من در اینجا معیار زیبایی شناختی حقیقت را به کار می‌گیرم، زیرا که من در اینجا از سادگی و زیبایی حرف می‌زنم، اما اذعان می‌کنم که برای من از آن سادگی و زیبایی گرته‌‌ی ریاضی، که طبیعت آن را به ما عرضه می‌کند، قدرت یقین بسیار زیادی بر می‌آید. شما خودتان هم این را تجربه کرده‌اید، که از آن سادگی و تمامیت روابط که طبیعت به یک‌باره پیش ما می‌گسترد و ما هم آمادگی دیدنش را نداریم، گاه می‌ترسیم!این احساس که از چنین مشاهده‌ای بر می‌خیزد، با آن احساسی که برآمده از شادمانی است، کاملا فرق دارد؛ آن احساسی که وقتی به ما دست می‌دهد، که گمان می‌کنیم کاری را، چه مربوط‌به فیزیک باشد و چه نباشد، خیلی خوب انجام داده‌ایم. به همین سبب هم مسلما امیدوارم، که آن دشواری‌هایی که پیش‌تر از آ‌‌ن‌ها حرف زدیم، به طریقی حل شود. سادگی گرته‌ی ریاضی افزون بر این، این نتیجه را هم در پی دارد، که این کار را ممکن می‌کند تا بسیاری از آزمایش‌هایی را نزد خود طرح کنیم که در آن‌ها می‌توانیم نتیجه را براساس نظریه با دقت زیاد پیش‌بینی کنیم. وقتی آن آزمایش‌ها را اجرا کردیم و نتیجه‌ای به بار آورد که پیش‌بینی کرده بودیم، دیگر اصلا جای شک برایمان باقی نمی‌ماند، که نظریه‌ی ما در این حوزه، طبیعت را به درستی می‌کند.

اینشتین هم رو به من کرد و گفت:

بازبینی از راه تجربه مسلما شرطی بدیهی بر درستی هر نظریه‌ای است. اما همه چیز را هم نمی‌توان آزمود. به همین سبب است که به آنچه درباره‌ی سادگی گفتید، بیشتر علاقه‌مندم. اما هیچ‌گاه هم ادعا نخواهم کرد که من درواقع آن چیزی را فهمیده‌ام که از سادگی قوانین طبیعت بر می‌آید!

پس از آن که این گفت و گو درباره‌ی معیارهای حقیقت در فیزیک بازهم مدتی به درازا کشید، با او خداحافظی کردم. بار دیگر که اینشتین را دیدم، یک سال ونیم بعد در اجلاس سولوی در بروکسل بود؛ جایی که مبانی معرفت شناختی و فلسفی این نظریه بار دیگر موضوع بحث‌هایی بسیار هیجان آور بود.

پایان قسمت اول

پیشنهاد می‌شود که پس از گذشت ۲۴ ساعت از مطالعه این بخش، اقدام به مطالعه‌ی بخش دوم این مقاله کنید.

در هر اندازه‌گیری مقدار کمی عدم قطعیت وجود دارد. اگر طول میزی را با متری نواری اندازه‌گیری کنید، می‌توانید بگویید یک متر است، اما متر نواری می‌تواند، تا اندازه یک میلی متر را هم نشان دهد. زیرا اندازه‌ی کوچک‌ترین علامت روی آن، این مقدار است. بنابراین میز می‌تواند واقعا ۹۹٫۹ سانتی‌متر یا ۱۰۰٫۱ سانتی‌متر باشد و شما ندانید. خیلی ساده است، اگر فکر کنید عدم قطعیت بخاطر محدودیت وسیله اندازه‌گیری است؛ اما بیان هایزنبرگ کاملا متفاوت است. این بیان می‌گوید؛ دقت وسیله‌ی اندازه‌گیری شما هرچه باشد، باز هم هرگز نمی‌توانید مقدار دو کمیت تکانه و مکان را در یک زمان به‌طور دقیق بدانید. درست مانند آن که وقتی مکان یک شناگر را اندازه می‌گیرید، نمی‌توانید در همان لحظه سرعت او را هم بدانید. درواقع می‌توانید هر دو را به‌صورت تقریبی بدانید، اما به محض تمرکز بر یکی، دیگری نامعین می‌شود!

ورنر هایزنبرگ اصل عدم قطعیت را هنگامی که روی مبانی ریاضی مکانیک کوانتومی در مؤسسه‌ی نیلز بوهر در کپنهاگ مشغول بود، صورت‌بندی کرد. در سال ۱۹۲۵ میلادی، پس از انجام یک کار پیشروانه به همراه هندریک کرامرز، هایزنبرگ مکانیک ماتریسی را بنیان گذاشت، که سبب جایگزین شدن مکانیک مدرن کوانتومی به‌جای نظریه‌ی کوانتومی قدیمی که فاقد عمومیت بود شد. فرض اصلی بر این بود که مفهوم حرکت کلاسیک به اندازه‌ی کافی در سطح کوانتومی دقیق نیست و الکترون‌های اتمی آن‌گونه که در فیزیک کلاسیک از مفهوم حرکت برداشت می‌شود، در مدارهای دقیقا معین حرکت نمی‌کنند. در عوض، حرکت به شکل عجیبی پخش شده‌است؛ تبدیل فوریه‌ی زمان تنها شامل فرکانس‌هایی است، که در جهش‌های کوانتومی مشاهده می‌شود. مقاله هایزنبرگ هیچ کمیت مشاهده‌ناپذیری مانند مکان دقیق الکترون در مدار در هر زمان دلخواه را نمی‌پذیرد؛ او به نظریه‌پرداز تنها این اجازه را می‌دهد که درباره‌ی مولفه‌های تبدیل فوریه‌ی حرکت حرف بزند. از آنجا که مولفه‌های فوریه در فرکانس‌های کلاسیک تعریف نشده‌است، نمی‌توان از آن‌ها برای ساخت و تشریح مسیر دقیق حرکت الکترون استفاده کرد؛ در نتیجه فرمالیسم نمی‌تواند به این پرسش‌ها پاسخ قطعی بدهد که الکترون دقیقا در کجا است یا دقیقاً چه سرعتی دارد. برجسته‌ترین خاصیت ماتریس‌های نامتناهی هایزنبرگ برای مکان و تکانه این است که در عمل ضرب جابجایی‌ناپذیر هستند. مقدار انحراف از جابجایی‌پذیری توسط رابطه‌ی جابجایی هایزنبرگ مشخص می‌گردد:

این رابطه تعبیر شفاف و مشخصی در ابتدا نداشت. در مارس ۱۹۲۶ میلادی، هنگامی که هایزنبرگ در مؤسسه بوهر کار می‌کرد، متوجه شد که جابجایی‌ ناپذیری اشاره به اصل عدم قطعیت دارد و این یک تعبیر واضح از عدم جابجایی‌پذیری بود، که بعدها سنگ بنای تعبیری شد، که با نام تعبیر کپنهاگی مکانیک کوانتومی نامیده شد. هایزنبرگ نشان داد که رابطه‌ی جابجایی نشان از عدم قطعیت دارد، یا به زبان بوهر حاکی از مکملیت است. هر دو کمیتی که جابجایی‌ناپذیر هستند نمی‌توانند همزمان اندازه‌گیری شوند. هر چقدر که یکی دقیق‌تر اندازه‌گیری شود، دومی نامعین‌تر خواهد بود.

می‌توان مکملیت بین مکان و تکانه را به وسیله‌ی مفهوم دوگانگی موج-ذره‌ای درک کرد. اگر ذره که به وسیله‌ی یک موج صفحه‌ای توصیف می‌شود، از میان یک شکاف باریک عبور کند، مانند امواج آب که از یک کانال باریک عبور می‌کنند، ذره پراکنده می‌شود و موج آن با زوایایی مختلفی از شکاف خارج می‌شود (پراشیده می‌شود). هر چقدر که پهنای شکاف کمتر باشد، مقدار پراش بیشتر شده و عدم قطعیت تکانه به تبع آن افزایش می‌یابد.

هایزنبرگ در مقاله‌ی مشهور خود در سال ۱۹۲۷ اظهارات خود را با این عبارت بیان کرد؛ کمترین مقداری غیرقابل اجتناب آشفتگی تکانه که علت آن اندازه‌گیری مکان است؛ اما در آنجا او تعریف دقیق از عدم قطعیت‌های Δx و Δp نداد و در عوض تخمین‌های قابل قبولی در هر مورد ارائه کرد. او در سخنرانی خود در شیکاگو اصل خود را اندکی جرح و تعدیل کرد:

ولی کنراد بود که در سال ۱۹۲۷ اولین‌بار صورت مدرن رابطه را چنین ارائه کرد:

که در این رابطه σx و σp انحراف استاندارد (معیار) مکان و تکانه هستند. توجه شود که  و  یکسان نیستند. در تعریف کنراد  و  به وسیله‌ی تکرار اندازه‌گیری مکان ذره و تکانه ذره در سیستم به شکل یک کل و محاسبه‌ی انحراف میانگین آن اندازه‌گیری‌ها حاصل می‌شود و ازاین‌رو رابطه‌ی کنراد چیزی درباره‌ی اندازه‌گیری همزمان به ما نمی‌گوید. همچنین در این رابطه   ثابت کاهیده‌ی پلانک(در قسمت پنجم توضیح مبسوطی درباره‌ی این ثابت بنیادی داده شده است) است. این رابطه نشان می‌دهد که حاصل ضرب خطای اندازه‌گیری در اندازه‌گیری همزمان هر یک از این دو کمیت همیشه بزرگ‌تر از یک مقدار مثبت مشخص است و هیچ‌گاه نمی‌تواند صفر باشد. اصل عدم قطعیت یک محدودیت بنیادی را در میزان اطلاعاتی که می‌توانیم از یک سامانه‌ی فیزیکی بگیریم، بیان می‌کند.

 اصل عدم قطعیت اغلب اوقات به این صورت بیان می‌شود: اندازه‌گیری مکان ضرورتا تکانه ذره را آشفته می‌کند، و بر عکس.

این عبارت، اصل عدم قطعیت را به‌نوعی اثر مشاهده‌گر تبدیل می‌کند. این تبیین نادرست نیست و توسط هایزنبرگ و نیلز بوهر استفاده شده‌است. باید توجه داشت که هر دوی آن‌ها، کم و بیش در چارچوب فلسفی پوزیتیویسم منطقی می‌اندیشیدند. در این روش نگرش، ذات حقیقی یک سیستم فیزیکی، بدان گونه که وجود دارد، تنها با تن دادن به بهترین اندازه‌گیری ممکن تعریف می‌شود، اندازه‌گیری‌ای که علی‌الاصول قابل اجرا باشد. به عبارت دیگر، اگر یک خاصیت سیستم (علی‌الاصول) قابل اندازه‌گیری با دقتی بیشتر از یک حد معین نباشد، آنگاه این محدودیت یک محدودیتِ سیستم است و نه محدودیتِ دستگاه‌های اندازه‌گیری. پس هر گاه که آن‌ها از آشفتگی غیرقابل اجتناب در هر اندازه‌گیری قابل تصور حرف می‌زدند، منظورشان آشکارا، عدم قطعیت ذاتی سیستم بود و نه عدم قطعیت ابزارها و وسایل اندازه‌گیری!

امروزه پوزیتیویسم منطقی در بسیاری از موارد از رونق افتاده‌است و از همین رو تبیین اصل عدم قطعیت برحسب اثر مشاهده‌گر می‌تواند گمراه‌کننده باشد. برای یک شخص که به پوزیتیویسم منطقی اعتقاد ندارد، آشفتگی خاصیت ذاتی یک ذره نیست، بلکه مشخصه‌ی فرایند اندازه‌گیری است، نزد چنین فردی ذره به‌صورت نهانی دارای تکانه و مکان دقیقی است، اما ما به‌دلیل نداشتن ابزارهای مناسب نمی‌توانیم آن کمیت‌ها را به دست بیاوریم. چنین تعبیری قابل قبول در مکانیک کوانتوم استاندارد نیست، در مکانیک کوانتوم، حالت‌هایی که در آن سیستم دارای تکانه و مکان معین باشد، اصلا وجود ندارد.

تبیین اثر مشاهده‌گر می‌تواند به طریق دیگری هم موجب گمراهی شود، چرا که برخی اوقات خطا در اندازه‌گیری ذره سبب ایجاد آشفتگی می‌شود. مثلا اگر یک فیلم عکاسی بی عیب و نقص که یک سوراخ ریز در وسط آن قرار دارد را برای آشکارسازی فوتون استفاده کنیم، و فوتون تصادفا از درون آن سوراخ عبور کند، با اینکه هیچ مشاهده‌ی مستقیمی از مکان ذره انجام نشده‌است، اما تکانه آن نامعین خواهد شد؛ که این استدلال از دیدگاه کپنهاگی نادرست است، چرا که عبور ذره از میان سوراخ، سبب تعین مکان شده و طبق اصل عدم قطعیت در آن هنگام تکانه نامتعین است. همچنین ممکن است استدلال شود که، پس از عبور فوتون از سوراخ اگر تکانه را اندازه بگیریم، می‌توانیم به تکانه ذره هنگام عبور از سوراخ پی ببریم و در این حالت هم تکانه و هم مکان ذره را با دقت نامحدود اندازه گرفته‌ایم. پاسخ صریح هایزنبرگ به چنین استدلالی این است، که اگر تکانه دقیقا در لحظه‌ی عبور از سوراخ اندازه‌گیری نشود، اصلا تعین نداشته‌است و اندازه‌گیری در آینده چیزی از واقعیتی که گذشته‌است را معین نمی‌کند. تبیین مذکور به طریق دیگری هم می‌تواند موجب گمراهی شود. به‌دلیل سرشت ناموضعِ حالت‌های کوانتومی، دو ذره که در هم تنیده شده‌اند را می‌تواند از هم جدا کرد و اندازه‌گیری را در فقط روی یکی از آن دو انجام داد. این اندازه‌گیری هیچ آشفتگی‌ای به معنای کلاسیکی‌ را در ذره‌ی دیگر ایجاد نمی‌کند، اما می‌تواند اطلاعاتی درباره‌ی آن آشکار سازد و بدین طریق می‌تواند مقدار مکان و تکانه را با دقت نامحدود اندازه‌گیری کرد.

برخلاف سایر مثال‌ها، اندازه‌گیری به این طریق هرگز سبب تغییر توزیع مقدار مکان یا تکانه کل نمی‌شود. توزیع تنها هنگامی تغییر می‌کند، که نتایج اندازه‌گیری از راه دور معلوم شود. اندازه‌گیری از راه دور مخفیانه (به طوری که ذره‌ی دیگر آگاه نشود)، هیچ اثری بر توزیع تکانه یا مکان ندارد. اما اندازه‌گیری از راه دورِ تکانه می‌تواند اطلاعاتی را آشکار کند که سبب فروپاشی تابع موج کل می‌شود. این امر سبب محدود شدن توزیع مکان و تکانه می‌شود، وقتی که اطلاعات کلاسیک (نزد ذره‌ی دیگر) آشکار شده و (به آن) انتقال می‌یابد.

برای مثال اگر دو فوتون در دو راستای مخالف هم بر اثر فروپاشی یک پوزیترون تابیده شوند، تکانه‌های دو فوتون خلاف جهت هم خواهد بود. با اندازه‌گیری تکانه‌ی یک ذره، تکانه‌ی دیگری معین می‌شود و سبب می‌شود که توزیع تکانه‌ی آن دقیق‌تر شود و مکان آن را در عدم تعین رها خواهد کرد. اما برخلاف اندازه‌گیری موضعی (از نزدیک) این فرایند هرگز نمی‌تواند عدم قطعیت بیشتری در مکان ذره‌ی دوم، بیش از آن که قبلا وجود داشته ایجاد کند. تنها این امکان وجود دارد، که عدم قطعیت را به روش‌های مختلف محدود کرد، که بستگی به خاصیتی دارد که شما برای اندازه‌گیری ذره‌ی دور انتخاب می‌کنید. با محدود کردن عدم قطعیت در p به مقادیر بسیار کوچک، عدم قطعیتِ باقی‌مانده در x همچنان بزرگ خواهد بود. (به واقع، این مثال پایه‌ی بحث آلبرت انیشتین در مقاله‌ی EPR در سال ۱۹۳۵ بود) هایزنبرگ صرفا بر ریاضیاتِ مکانیک کوانتوم تمرکز نکرد و اساسا این دغدغه را داشت که پایه‌گذار این باور باشد، که عدم قطعیت یک مشخصه‌ی واقعی جهان است. برای این کار، او استدلالات فیزیکی خود را براساس وجود کوانتا و نه کل فرمالیسم مکانیک کوانتومی طرح‌ریزی کرد. او صرفا به فرمالیسم ریاضی بسنده نکرد و از آن برای توجیه چیزی استفاده نکرد، چرا که این خود فرمالیسم بود که نیاز به توجیه داشت!

مفهوم عمیق اصل عدم قطعیت، از دید هایزنبرگ پنهان نماند و او دریافت که این اصل چگونه با فیزیک مرسوم آن زمان در چالش است. پیش از هر چیز، این اصل نشان داد که رفتار گذشته یک ذره بنیادی تا زمانی‌که اندازه‌گیری روی آن صورت نگرفته مشخص نمی‌شود. طبق نظر هایزنبرگ؛ مسیر، تنها زمانی‌که ما آن را مورد مشاهده قرار می‌دهیم، به وجود می‌آید. ما تا زمانی‌که موقعیت چیزی را اندازه نگیریم نمی‌توانیم بفمیم کجاست. همچنین او اذعان داشت، که مسیر آینده یک ذره هم نمی‌تواند قابل پیش‌بینی باشد. به خاطر این عدم قطعیت‌های بزرگ و سرعت، در نتیجه آینده هم غیر قابل پیش‌بینی است.

هر دوی این بیانات شکاف عمیقی در فیزیک نیوتنی آن زمان که فرض؛ جهان خارج، به‌طور مستقل وجود دارد و یک ناظر فقط می‌تواند با اندازه‌گیری حقیقت آن را کشف کند، ایجاد کرد. مکانیک کوانتومی نشان داد که در سطح اتمی، چنین دیدگاه قطعی‌ای‌، بی‌معنی است و تنها می‌توان راجع به احتمال یک نتیجه صحبت کرد. دیگر نمی‌توانیم در مورد علت و اثر صحبت کنیم، چرا که فقط شانس دخیل است. پذیرش این موضوع برای اینشتین و بسیاری از دانشمندان دیگر سخت بود. اما مجبور بودند آنچه معادلات نشان می‌دهد را قبول کنند. برای اولین‌بار، فیزیکدانان از قلمروی آزمایشگاه تجربی پا را فراتر نهاده و به سوی قلمرو ریاضیات انتزاعی پیش رفتند.

هایزنبرگ به‌دلیل تنظیم اصل عدم قطعیت، در سال ۱۹۳۲ میلادی جایزه نوبل فیزیک را به خود اختصاص داد. وی علاوه‌بر جایزه نوبل موفق به کسب افتخارات بسیاری شد از جمله آن‌ها؛ او به‌عنوان عضو جامعه‌ی سلطنتی شهر لندن، که درآن زمان افتخار بسیار بزرگی در کشور انگلستان به حساب می‌آمد دست یافت و همچنین به‌عنوان عضو آکادمی(هیئت علمی دانشگاه) بسیاری از شهرهای کشورهای اروپایی درآمد. ولی در میان این همه شاید گران بهاترین پاداش به وی جایزه کوپرنیک به حساب آید.

در یکی از شب‌هایی که به مناسبت تشکیل اجلاس سولوی همگی در بروکسل و در هتل بودیم، بعضی از اعضای جوان‌تر اجلاس، پس از رفتن دیگران، هنوز در سالن ورودی هتل نشسته بودند. من و ولفگانگ پائولی هم در آن جمع بودیم و کمی بعد هم پل دیراک به ما پیوست. یکی از ما این سؤال را مطرح کرد؛

 اینشتین خیلی زیاد درباره‌ی خدا حرف می‌زند، این حرف‌ها چه معنایی دارد؟ درواقع نمی‌توان تصور کرد که دانشمندی مثل اینشتین این قدر دلبستگی‌اش به یکی از آیین‌های دینی زیاد باشد.

 در جواب یکی گفت:

 اینشتین مسلما نه، اما شاید ماکس پلانک!

درباره‌ی رابطه علم و دین از پلانک گفته‌هایی هست، که بنا بر آن‌ها نظر او این است که هیچ‌گونه تضادی میان این دو وجود ندارد، بلکه علم و دین به خوبی با یکدیگر سازگار هستند. از من سؤال شد چه چیزی از نظر پلانک در این حوزه می‌دانم و درباره‌ی آن چه فکر می‌کنم؟ من چند دفعه البته با پلانک شخصا صحبت کرده بودم؛ آن حرف‌ها هم بیشتر درباره فیزیک بود و به مسائل کلی نمی‌پرداخت، اما از دوستان صمیمی پلانک چند نفری را می‌شناختم، که از او به من خیلی چیزها گفته بودند و به همین جهت هم گمان می‌کردم که می‌توانم تصویری از نظر او ارائه دهم، بنابراین شاید اینطور گفتم:

گمان می‌کنم که علم و دین از نظر پلانک به این علت باهم سازگار است، چون این دو، آن طور که پیش فرض اوست، به حوزه‌های کاملا متفاوت از واقعیت مربوط می‌شود. علم به کار جهان مادی عینی می‌پردازد. علم ما را دربرابر این وظیفه قرار می‌دهد، تا اخبار درست درباره این واقعیت عینی بدهیم و ارتباطات درونی آن‌ها را درک کنیم. اما دین به دنیای ارزش‌ها می‌پردازد. در اینجا از آن چیزی صحبت می‌شود که باید باشد، که ما باید انجام دهیم، اما نه از آنچه هست. در علم حرف از درست و نادرست است، در دین از خوب و بد، از با ارزش و بی ارزش. علم اساس عمل فنی سودمند است، دین اساس اخلاق است. پس به نظر می‌رسد نزاع میان این دو حوزه از سده‌ی هجدهم تاکنون بر آن سوء فهمی استوار باشد، که زمانی پدیدار می‌شود که بخواهیم رمز و تمثیل‌های دین را به‌عنوان ادعاهای علمی تفسیر کنیم؛ کاری که مسلما بی معنی است! در این نظر، که من آن را نزد پدر و مادرم به خوبی می‌دیدم، این دو حوزه‌ی جدا ازهم، وجه عینی و وجه ذهنی عالم به شمار می‌آید. علم کم و بیش شیوه‌ای است، که ما با وجه عینی واقعیت رو در رو می‌شویم، شیوه‌ای است که ما با آن جدل می‌کنیم، عقیده‌ی دینی به عکس بیان تصمیمی ذهنی است، که بنا بر آن ما برای خود ارزش‌هایی را معین می‌کنیم، تا به عمل خود در زندگی مطابق آن‌ها جهت بدهیم. ما این تصمیم را البته بنا بر قاعده در مطابقه با جمعی می‌گیریم، که به آن تعلق داریم، این جمع چه خانواده باشد، چه ملت یا گروه فرهنگی تربیت و محیط، بر این تصمیم بیشترین تأثیر را دارد. اما این تصمیم سرانجام تصمیمی ذهنی است و به همین سبب هم نمی‌توان معیار درست یا نادرست را در مورد آن به کار برد. ماکس پلانک، اگر نظرش را درست فهمیده باشم، از این آزادی استفاده کرد و به‌طور روشن آیین مسیحی را برگزید. فکر و عمل او، به‌خصوص در روابط اجتماعی‌اش هم، بی قید و شرط در چهارچوب این آیین محقق می‌شود و از این جهت هم هیچکس نمی‌تواند از احترام به او کوتاهی کند. به این ترتیب هر دو حوزه، یعنی وجه عینی جهان و وجه ذهنی جهان، به‌طور کاملا روشن، از هم جداست، اما باید اعتراف کنم که من این جدایی را نمی‌پسندم. شک دارم که جوامع انسانی بتواند در دراز مدت با این شکاف روشن میان علم و ایمان سر کند.

 ولفگانگ که نگرانی من را درست می‌دانست، گفت:

نه، این وضع چندان هم نمی‌تواند خوب پیش برود. در آن زمانی‌که ادیان پدیدار شد، مسلما کل معرفتی که در اختیار جامعه مربوط بود، در آن قالب فکری‌ای هم می‌گنجید، که مهم‌ترین محتوای آن ارزش‌ها و افکار آن دین بود. خواست ما از این قالب فکری این بود، که حتی برای ساده‌ترین فرد جامعه هم به نحوی فهمیدنی باشد، حتی اگر آن رمز و تمثیل‌ها به او تنها احساسی مبهم از آن چیزی می‌داد که درواقع منظور آن ارزش‌ها و افکار بود. انسان عادی باید یقین داشته باشد که اگر بخواهد تصمیم هایش در زندگی را براساس آن ارزش‌ها بگیرد، آن قالب فکری برای همه‌ی معرفت جامعه کفایت می‌کند. چون برای این انسان، ایمان به معنای، درست انگاشتن نیست، بلکه به این معنا است؛ که راهنمایی خود را به این ارزش‌ها بسپارد. اما اگر قرار باشد که معرفت تازه، که در سیر تاریخ به دست می‌آید، قالب فکری قدیم را تهدید به انفجار از درون کند، آن وقت خطرهای بزرگی به وجود می‌آید. پس جدایی کامل میان ایمان و معرفت به یقین فقط کمکی اضطراری برای زمانی بسیار محدود است. برای نمونه، در مجموعه‌ی فرهنگی غرب در آینده‌ای نه چندان دور، ممکن است آن لحظه‌ای فرا رسد، که دیگر رمز و تمثیل‌های دین پیشین حتی برای انسان عادی هم قدرت یقین نداشته باشد و بعد، آن طور که من از آن بیم دارم، اخلاق پیشین هم در کوتاه‌ترین زمانی فرو ریزد و چیزهایی ترسناکی پیش بیاید که اکنون حتی تصور آن‌ها را هم نتوانیم، بکنیم. بنابراین با فلسفه‌ی پلانک نمی‌شود چندان کاری از پیش برد، حتی اگر منطقا درست باشد، اگرچه به آن نگرشش به انسان هم، که از آن نتیجه می‌شود، احترام می‌گذارم. نظر اینشتین برایم بیشتر آشناست. آن خدایی که او خیلی هم با رغبت از آن یاد می‌کند، به نحوی با قوانین تغییرناپذیر طبیعت سرو کار دارد. اینشتین با این نظم درونی اشیا به‌نوعی همدل است. او این نظم را در سادگی قوانین طبیعت حس می‌کند. می‌توان گمان برد که او خود این سادگی را با کشف نظریه‌ی نسبیت، عمیقا و به‌طور مستقیم آزموده بود. اما از اینجا تا محتوای ادیان، البته بازهم راهی طولانی است. اینشتین چندان هم به آیینی مذهبی دلبستگی نداشت و من هم عقیده دارم که او شاید با تصور خدایی متشخص کاملا ناآشنا باشد. اما برای او هیج جدایی‌ای هم میان دین و علم وجود ندارد. نظم درونی در نظر او، هم در حوزه عینی است و هم در حوزه‌ی ذهنی و این شاید نقطه شروع بهتری باشد.

 با لحنی اعتراض آمیز پرسیدم؛

 نقطه شروع چه کاری؟ اگر این نگاه به نظام کل را مثلا امری کاملا شخصی بدانیم، آن وقت نظر اینشتین را البته خیلی خوب هم می‌توانیم بفهمیم، اما باز هم از این نگرش اصلا چیزی عاید نمی‌شود.

ولفگانگ در جواب گفت:

چرا، شاید هم چیزی به دست بیاید. گسترش علم در دو سده‌ی اخیر مسلما فکر انسان را در کل تغییر داده است و این تغییر از محدوده‌ی فرهنگی مسیحی هم فراتر رفته است. پس این نکته هم چندان بی‌اهمیت نیست که فیزیکدانان چه نظری دارند و از قضا درست همین تنگنای آرمان ما از جهان عینی است، که در زمان و مکان بنا بر قانون علیت حرکت می‌کند، که این ستیز با قالب‌های فکری ادیان مختلف را برانگیخته است. وقتی علم خود این چهار چوب تنگ را متلاشی می‌کند، چنان که با نظریه‌ی نسبیت همین کار را کرد و شاید هم روزی با نظریه کوانتومی، که حالا درباره‌ی آن با حرارت بحث می‌کنیم، بیشتر از این‌ها بکند، رابطه‌ی میان علم و محتوایی که ادیان در قالب فکری خود در پی آنند، باز هم طور دیگری در چشم ما نمایان می‌شود. شاید با آن روابط درونی‌ای که در سی سال اخیر در علم آموخته‌ایم، افق فکری وسیع‌تری نصیبمان شده باشد. مثلا مفهوم مکملی، که نیلز بور در تفسیر نظریه‌ی کوانتومی این روزها این قدر به آن اهمیت می‌دهد، در علوم انسانی و در فلسفه اصلا چیز ناشناخته‌ای نبود، هر چند در اینجا به صراحت صورت‌بندی نشده باشد. اما اینکه این مفهوم در علوم دقیقه پیدا شود، به‌معنی تغییری قاطع است؛ زیرا که به کمک این مفهوم است که از همان آغاز می‌توان این نکته را روشن کرد که آن تصوری که ما از شی مادی داریم، که در آن، شی از اینکه به چه صورتی مشاهده می‌شود کاملا مستقل است، تنها نمایانگر تعمیمی انتزاعی است که با آن هیچ واقعیتی به درستی مطابقت ندارد. در فلسفه‌ی آسیایی و در ادیان این سرزمین‌ها نیز تصوری مکملی از ذهن شناسای محض وجود دارد که دربرابر آن دیگر هیچ عینی نیست. این تصور هم خود نشانگر نوعی تعمیم انتزاعی است، که با آن هیچ‌گونه واقعیت فکری یا ذهنی مطابقت نمی‌کند. تفکر درباره نظام‌های بزرگ ما را در آینده ناچار می‌کند، تا موضع حد وسط را (آنچه نظریه مکملی بور نشان می‌دهد) بگیریم. علمی که خود را با این شیوه‌ی فکر کردن تطابق داده است، نه فقط دربرابر صورت‌های مختلف دین مدارا پیشه می‌کند، بلکه شاید هم بتواند، چون کل را بهتر می‌بیند، به دنیای ارزش‌ها کمک کند.

در حین این بحث‌ها، پاول دیراک هم پیش ما نشست. دیراک که در آن زمان تازه بیست و پنج سال داشت و از مدارا هم خیلی مایه‌ای نداشت، گفت:

نمی‌دانم چرا اینجا از دین حرف می زنیم. اگر کسی صادق باشد و دانشمند هم باید به‌خصوص صادق باشد، باید بپذیرد که در دین ادعاهای نادرست آشکاری بیان شده است، که آن‌ها را در واقعیت اصلا نمی‌توان توجیه کرد. مثلا مفهوم خدا، خودش محصول خیال بشر است. این نکته را می‌شود فهمید که انسان‌های اولیه، که بیش از ما در معرض قهر نیروهای طبیعت بوده‌اند، از ترس به این نیروها تشخص داده باشند و بعد هم به مفهوم خداوندی رسیده باشند. اما در دنیای ما، در دنیایی که روابط درونی طبیعت را می‌توانیم بفهمیم، دیگر به چنین تصوراتی نیازی نیست. من نمی‌توانم بفهمم که فرض وجود خدایی قادر بتواند به نحوی به ما کمک کند؛ اما به درستی می‌توانم بفهمم که قبول این فرض به پرسش‌های بی‌معنایی بینجامد. به‌طور مثال؛ به این سؤال که چرا خدا به بدبختی و بی‌عدالتی در دنیای ما اجازه بروز داده است، چرا دست اغنیا را باز می‌گذارد تا به فقرا ستم کنند یا چرا دیگر سختی‌های روزگار وجود دارد، درحالی‌که می‌تواند از آن‌ها جلوگیری کند. اگر در زمان ما هنوز درس دین داده می‌شود، این امر مسلما به این دلیل نیست که این تصورات هنوز هم می‌تواند در ما یقین برانگیزد، بلکه در پس آن این میل وجود دارد، تا مردم را و خاطر انسان‌های ساده را تسلی دهد. بر انسان‌های آرام، ساده‌تر می‌توان حکومت کرد تا بر مردم ناآرام و ناراضی. از انسان آرام، ساده‌تر می‌توان سوءاستفاده کرد، او را ساده‌تر می‌توان استثمار کرد. دین نوعی افیون است که به مردم می‌دهند، تا آن‌ها را با رویاهای شیرین خواب کنند و با این کار آن‌ها را از دست آن بی‌عدالتی‌ای آرام کنند، که بر سر آن‌ها می‌آید و از همین زمان است، که اتحاد میان دو قدرت بزرگ سیاسی، یعنی دولت و کلیسا، به آسانی پدیدار می‌شود. هر دو به این توهم نیاز دارند که خدای مهربانی، هر چند که روی زمین نباشد، به یقین در آسمان هاست، تا به آن کسانی پاداش دهد که بر ضد بی‌عدالتی ایستادگی نکرده‌اند، که آرام و صبور وظایف خود را انجام داده‌اند. صادقانه بگوییم، این خدا که تنها محصولی از خیال بشر است، باید طبیعتا بدترین گناه کبیره شمرده شود.

 رو به دیراک کردم و گفتم:

 به این ترتیب قضاوت تو از دین بر پایه‌ی سوءاستفاده سیاسی است و چون می‌توان تقریبا از هر چیزی در این دنیا سوءاستفاده کرد. حتی از مرام کمونیستی که تو از آن اخیر صحبت می‌کردی، چنین قضاوتی در باره‌ی این مسئله به حق نیست. همیشه هم بالاخره جوامع بشری وجود دارند و چنین جوامعی هم باید زبان مشترکی بیابند، تا بتوانند با آن درباره مرگ و زندگی و آن نظام بزرگ صحبت کنند، که ذیل آن زندگی در جامعه جریان دارد. آن قالب‌های فکری، که در پی جستجوی زبانی مشترک در طول زمان رشد کرده است، باید هم قدرت یقین زیادی داشته باشد، تا این همه انسان طی سده‌ها زندگی خود را بنا بر آن قالب‌ها سروسامان داده باشند. پس به همین سادگی هم که تو می‌گویی، دین از دور خارج نمی‌شود. اما شاید برای تو دین دیگری باشد، مثلا دین قدیمی چین، که قدرت یقین بیشتری دارد تا آن دینی که در آن تصور خدای متشخص پیش می‌آید.

دیراک در جواب گفت:

من اصلا نمی‌توانم از اساطیر دینی چیزی سر دربیاورم، چون اساطیر ادیان مختلف باهم ضد و نقیض است. این هم اصلا تصادف محض است که من در اروپا به دنیا آمده‌ام و نه در آسیا و اینکه چه چیز حقیقت است و من هم باید به چه چیز اعتقاد داشته باشم، نمی‌تواند وابسته به آن باشد. من فقط می‌توانم به آن چیزی اعتقاد داشته باشم که حقیقت است. اینکه چگونه باید رفتار کنم، فقط آن را منحصرا با استفاده از عقل می‌توانم در آن موقعیتی نتیجه بگیرم، که اگر در جمعی با دیگران زندگی می‌کنم، در آن جمع، باید برای افراد آن همان قدر حق زندگی قائل باشم، که برای خود قائلم. پس باید تلاش کنم تا موازنه در منافع همگان به وجه عادلانه‌ای تأمین شود؛ بیش از این به چیزی نیاز نیست. پس تمام حرف‌هایی که درباره‌ی اراده خدا، گناه و عقوبت و دنیای دیگر گفته می‌شود، تا ما به رفتارمان بنابر آن جهت دهیم، فقط به اختفای واقعیت خشن و عریان خدمت می‌کند. اعتقاد به وجود خدا به این تصور هم میدان می‌دهد، که این خواست خداست تا دربرابر قدرت بالادست سر تعظیم فرود بیاوریم و به همین ترتیب است، که دوباره آن ساخت‌های اجتماعی‌ای ماندنی می‌شود که در گذشته شاید طبیعی بوده، اما امروز دیگر مناسب دنیای ما نیست. حقیقت این است که حتی از صحبت درباره‌ی نظام بزرگ یا مانند آن اکراه دارم. زندگی هم درست مثل علم است؛ در مقابل مشکلات قرار می‌گیریم، پس باید سعی کنیم آن‌ها را حل کنیم، اما همیشه می‌توانیم فقط یک مشکل را و نه چند مشکل را باهم حل کنیم؛ پس در اینجا صحبت از نظام بزرگ، به معنای صحبت از فراساخت فکری‌ای است، که متأخر است.

 بحث ما باز هم مدتی از اینجا به آنجا کشیده شد و تعجب هم می‌کردیم، که ولفگانگ دیگر در بحث شرکت نمی‌کند؛ فقط گوش می‌کند، گاهی با چهره‌ای کمی ناراضی، گاهی هم با لبخندی شیطنت آمیز، اما اصلا هم حرفی نمی‌زند. سرانجام از او نظرش را پرسیدیم. با تعجب نگاهی کرد و گفت:

 بله، بله، دوست ما دیراک هم دینی دارد؛ اساس این دین این است؛ خدایی وجود ندارد و دیراک هم فرستاده‌ی اوست.

ما هم، از جمله خود دیراک، خندیدیم و گفتگوی آن شب ما هم در سالن هتل به پایان رسید.

چندی بعد، شاید هم در کپنهاگ باشد، که حرف‌های آن شب را برای نیلز تعریف کردم. نیلز فورا به دفاع از این جوان‌ترین عضو جمع ما بر آمد، و گفت:

چه عالی است که پل دیراک بی‌آنکه کوتاه بیاید، از چیزی جانبداری می‌کند که به زبان منطق کاملا بیان شدنی است. حرفش این است که آنچه اصولا بیان شدنی باشد، به روشنی هم بیان می‌شود و برای اینکه حرف ویتگنشتاین را گفته باشم، درباره‌ی آنچه نمی‌توان حرف زد، باید خاموش ماند. وقتی دیراک کار جدیدی به من ارائه می‌دهد، دست نوشته‌اش به‌حدی خوانا و بدون خط خوردگی است که حتی دیدن آن حظی بصری است و حتی وقتی به او پیشنهاد می‌کنم، که این یا آن صورت‌بندی را تغییر دهد، کاملا دل آزرده می‌شود و در بیشتر موارد هم اصلا چیزی را تغییر نمی‌دهد. درهرصورت کارش این طور یا آن طور هم بسیار عالی است. همین تازگی‌ها با او به نمایشگاهی از آثار هنری رفته بودم، که منظره‌ای از طبیعت ایتالیا از مانه‌ی نقاش در آنجا آویخته بود؛ منظره‌ای از کنار دریا با زمینه‌ی آبی متمایل به خاکستری دلپذیر. در جلو قایقی دیده می‌شد و نزدیک آن روی آب لکه خاکستری متمایل به سیاهی که معنای آن هم به‌سادگی فهمیده نمی‌شد. دیراک دراین مورد گفت؛ این لکه سیاه به جا نیست. این طرز نگاه کردن به آثار هنری، مسلما شیوه غریبی است. اما حق کاملا با او بود. در کار هنری خوب، درست مثل کار علمی خوب، باید هر یک از جزئیات به روشنی مشخص باشد و هیچ چیز هم نباید تصادفی باشد.با وجود همه‌ی این‌ها، درباره‌ی دین اصلا نمی‌شود، این طور حرف زد. برای من هم، درست مثل دیراک است، یعنی برای من هم تصور خدای متشخص ناآشناست. این مورد هم باید به‌خصوص کاملا روشن باشد که زبان در دین به شیوه‌ای به کار می‌رود که کاملا با استفاده‌ی آن در علم متفاوت است. زبان دین با زبان شعر نزدیکی بیشتری دارد، تا با زبان علم. در حال حاضر هم البته تمایل به این سو است، که گمان کنیم علم به اطلاعات درباره‌ی امر واقع عینی می‌پردازد و شعر به موضوع بیدارشدن احساسات درونی. در دین حرف از حقیقت عینی است، پس باید این حقیقت از معیارهای حقیقت علمی تبعیت کند. به نظرم می‌رسد که همه این تقسیم عالم به وجه ذهنی و وجه عینی در اینجا بیش از اندازه عُنفی باشد. اینکه در ادیان همه زمان‌ها به زبان تمثیل و رمز و شطح حرف زده شده است، معنایی جز این ندارد؛ که امکانات دیگری وجود ندارد تا آن واقعیتی را درک کنیم که در دین گفته شده است. اما این هم به این معنا نیست که این واقعیتی اصیل نیست. با تقسیم واقعیت به وجهی عینی و وجهی ذهنی، کار چندانی نمی‌توان از پیش برد. به همین سبب هم این را نوعی آزادی در فکر می‌بینم، که از پیشرفت فیزیک در دهه‌های اخیر یاد گرفته‌ایم، که مفاهیم عینی و ذهنی تاچه حد ابهام دارد و این وضع هم در آغاز با نظریه‌ی نسبیت شروع شد. پیش‌تر این خبر که دو پدیده هم زمان باشد، به معنای تصریحی عینی بود که می‌توانستیم آن را به زبان به روشنی برای دیگری بازگو کنیم و با این کار هم بازبینی آن را برای هر ناظر دلخواهی ممکن کنیم. اما امروز می‌دانیم که مفهوم هم زمانی عنصری ذهنی دارد، تا جایی که دو رویداد که برای ناظری ساکن هم زمان است، برای ناظری متحرک الزاما هم زمان نیست. تشریح این مسئله با نظریه نسبیت هم تا این حد عینی است، چون هر ناظری می‌تواند با محاسبه به ناظر دیگری خبر دهد، که چه چیزی را مشاهده خواهد کرد یا پیش‌تر مشاهده کرده است. پس در اینجا هم از آرمان تشریحی عینی به مفهوم پیشین آن در فیزیک کلاسیک، بازهم چند قدمی دور شده‌ایم. در مکانیک کوانتومی روی گردانی از این آرمان، باز هم با قاطعیت بیشتری پیش رفت. آنچه در اینجا می‌توانیم به زبانی که گویای واقعیت عینی به معنای فیزیک کلاسیک باشد، به دیگری انتقال دهیم، فقط اخباری درباره امر واقع است. مثلا در این حدود که بگوییم؛ در اینجا صفحه‌ی عکاسی سیاه شده است، یا در اینجا قطره‌های آب تشکیل شده است. از خود اتم در اینجا چیزی گفته نمی‌شود. اما آنچه از این تصریح در آینده کسب می‌شود، به طرح تجربی سؤالی وابسته است که ناظر آن را آزادانه انتخاب می‌کند و طبعا هم فرقی نمی‌کند که ناظر انسان یا حیوان یا دستگاه باشد. اما پیش‌بینی آنچه در آینده روی خواهد داد، نمی‌تواند بدون ارجاع به آن ناظر یا آن ابزار مشاهده بیان شود. پس تا اینجا در حال حاضر در علم، هر امر واقع فیزیکی خصیصه‌های عینی و ذهنی هردو را دارد. جهان عینی علم در سده‌ی پیش، آن طور که اکنون می‌دانیم، واقعیت نبود، بلکه مفهوم حدی آرمانی بود. هر جدلی با واقعیت، در آینده هم مسلما این ضرورت را پیش می‌آورد، تا میان وجه عینی و وجه ذهنی فرق بگذاریم، یعنی میان آن دو خط فاصلی بکشیم. اما موقعیت این خط فاصل، می‌تواند به شیوه مشاهده وابسته باشد، تاحدودی به دلخواه انتخاب شود. به این سبب، می‌توانم این نکته را درست درک کنم، که چرا نمی‌توان درباره‌ی محتوای دین به زبانی حرف زد که واقعیت عینی را بیان کند. این واقعیت که ادیان مختلف در پی آن بر می‌آیند، تا این محتوا را در قالب‌های فکری کاملا متفاوت بریزند، به هیچ وجه به معنای ایرادی برضد کِنه واقعی دین نیست. شاید بتوان این قالب‌های متفاوت را شیوه‌های تشریحی مکمل یکدیگر دانست، که هر چند متقابلا یکدیگر را نفی می‌کنند، اما از آغاز در کلیت خود تصویری از آن غنایی به دست می‌دهد، که برگرفته از رابطه‌ی انسان با نظام بزرگ است.

در ادامه صحبت گفتم:

وقتی تو زبان دین را این قدر روشن از زبان علم و زبان هنر جدا می‌کنی، پس آن احکامی که اغلب هم با قاطعیت اعلام می‌شود، مانند اینکه خدای حی و حاضری وجود دارد، یا اینکه روحی لایموت وجود دارد، به چه معنایی است؟ در این زبان کلمه وجود دارد به چه معنایی است؟ ما می‌دانیم که نقد از علم، از جمله نقد دیراک از علم، درست برضد چنین عباراتی است. اجازه بده برای اینکه اول به وجه معرفت شناختی نظری مسئله بپردازیم، این مقایسه را انجام دهیم همان‌طور که می‌دانی، در ریاضیات با واحدی موهومی، یعنی با ریشه دوم ۱- که به‌صورت 1-√ نوشته می‌شود، سر و کار داریم و برای معرفی آن، نشانه i را به کار می‌گیریم. این را هم می‌دانیم که این عدد، در بین اعداد طبیعی وجود ندارد. با وجود این شاخه‌های مهمی از ریاضیات، مثلا همه‌ی نظریه توابع تحلیلی، بر معرفی این واحد موهومی استوار است و این هم به معنای آن است که 1-√ متأخرا وجود دارد. تو هم با من موافقی که وقتی می‌گویم 1-√ وجود دارد، این جمله به معنای چیزی جز این نیست، که روابط مهمی در ریاضیات وجود دارد که آن‌ها را می‌توان با معرفی مفهوم 1-√ به ساده ترین صورتی نمایاند. اما این روابط بدون معرفی هم وجود دارد؛ به همین سبب می‌توان از این نوع ریاضیات هم در علوم طبیعی و فنون، عملا به خوبی استفاده کرد. مثلا در نظریه توابع آنچه اهمیت دارد، وجود قانونمندی‌های ریاضی مهمی است، که بر زوجی از متغیرهای پیوسته استوار است. وقتی مفهوم انتزاعی 1-√ را می‌سازیم، این روابط ساده‌تر فهمیده می‌شود، گرچه این مفهوم برای درک مطلب اساسا ضروری نیست و میان اعداد طبیعی هم برایش همتایی وجود ندارد. مفهوم انتزاعی مشابه دیگری در ریاضیات، مفهوم بی‌نهایت است که آن هم در ریاضیات جدید اهمیت زیادی دارد، گرچه با آن هم هیچ چیز مطابقت نمی‌کند و تازه با ورودش در ریاضیات هم خود را به دردسر بزرگی دچار کرده‌ایم. بنابراین در ریاضیات پیوسته به مرحله انتزاعی بالاتری می‌رویم و از این راه هم به فهمی یکپارچه از حوزه وسیع‌تری می‌رسیم. آیا می‌توانیم برای اینکه به نقطه شروع سؤال برگردیم، کلمه وجود دارد را در دین هم به معنای رفتن به مرحله‌ی انتزاعی بالاتری بدانیم؟ این رفتن به مرحله‌ی بالاتر هم باید، کار را بر ما آسان‌تر کند تا روابط در جهان را بفهمیم و نه بیشتر. اما آن روابط هم همیشه به واقع وجود دارد و برای آن‌ها هم فرق نمی‌کند، که ما با چه قالب‌های فکری می‌خواهیم آن‌ها را درک کنیم.

 بور در جواب گفت:

تا آنجا که حرف از وجه معرفت شناختی مسئله است، شاید این مقایسه خوب پیش برود. اما از دیدگاه دیگری این مقایسه ناقص است. در ریاضیات می‌توانیم خود را در فکر از محتوای احکام دور نگاه داریم و سرانجام هم این امر به بازی فکری‌ای می‌ماند که می‌توانیم در آن شرکت کنیم یا خود را از شرکت در آن محروم کنیم. اما در دین مسئله به خود ما مربوط می‌شود، به زندگی ما و به مرگ ما، چون در این جا احکام اعتقادی به مبادی رفتار ما تعلق دارد و دست کم غیر مستقیم به مبادی وجودی ما؛ پس ما هم نمی‌توانیم از دور فقط نظاره کنیم و نگرش ما هم به مسائل دین اصلا نمی‌تواند از جایگاه ما در جامعه بشری جدا باشد. وقتی دین به‌عنوان ساختار فکری در جامعه‌ای از انسان‌ها پدیدار شد، شاید بازهم جایی برای این پرسش باقی بماند، که آیا باید در جریان تاریخ به دین به‌عنوان قوی‌ترین نیروی سازنده جامعه نگریست، یا آن که جامعه‌ای که حالا وجود دارد ساختار فکری خود را می‌سازد و گسترش می‌دهد و خود را با معرفت کنونی‌اش سازگار می‌کند. به نظر می‌رسد که فرد در زمان ما کاملا آزادانه می‌تواند، انتخاب کند که باتوجه‌به فکرش و رفتارش، خود را در کدام یک از ساختارهای فکری جا دهد و در این آزادی این واقعیت بازتاب دارد که، جُمود در مرزهای حوزه‌های فرهنگی مختلف و در جوامع بشری رو به سستی دارد و این مرزها رو به روان شدن. اما حتی زمانی‌که این فرد می‌کوشد تا بیشترین استقلال را به دست آورد، باز هم ناگزیر است از ساختارهای فکری موجود، آگاهانه یا ناآگاهانه، چیزهای زیادی بگیرد، چون او باز هم باید بتواند با اعضای دیگر جامعه‌اش، که در آن تصمیم به زندگی گرفته است، درباره‌ی زندگی و مرگ و درباره روابط کلی صحبت کند. او باید فرزندانش را بنابر سرمشق‌های جامعه تربیت کند، او باید برای خود در زندگی کلی جامعه‌اش جایی بیابد و اینجا است که دیگر آن ظرافت‌های معرفت شناختی اصلا به کارش نمی‌آید. ما در اینجا هم باید کاملا آگاه باشیم، که رابطه‌ای مکملی میان تفکر انتقادی درباره محتوای عقیدتی دین و عملی که پیش شرط تصمیم به انتخاب ساختار فکری آن دین است وجود دارد، از اجرای آگاهانه تصمیمی که فرد می‌گیرد، نیرویی حاصل می‌شود که او را در رفتارش راهبری می‌کند، به او در پریشانی خاطر کمک می‌کند، اگر رنجی ببیند، او را تسلی می‌دهد، به طوری که احساس امنیت در نظام بزرگ ضامن آن می‌شود، این طور است که دین به هماهنگ شدن زندگی با جامعه کمک می‌کند و از مهم‌ترین کارهایش این است، تا در زبانش به استعاره و رمز، نظام بزرگ را یادآوری کند.

در دنباله‌ی سؤالم گفتم:

 تو خیلی از انتخاب آزاد فرد صحبت می‌کنی و وقتی آن را با فیزیک اتمی مقایسه می‌کنی، مثل این است که تو این انتخاب آزاد را با آزادی ناظری می‌سنجی که می‌تواند تجربه‌اش را به این صورت یا آن صورت انجام دهد. شاید در فیزیک کلاسیک برای چنین مقایسه‌ای جایی وجود نداشته باشد. اما آیا حاضری خصیصه‌های ویژه فیزیک امروز را حتی مستقیم‌تر به مسئله‌ی آزادی اراده مربوط کنی؟ تو میدانی که جبری نبودن کامل پدیده‌ها در فیزیک اتمی گاهی هم چون دلیلی به کار گرفته می‌شود، گویی که برای آزادی اراده‌ی فرد و مداخله خدا دوباره جایی باز شده است.

بور در جواب گفت:

من یقین دارم که در این جا به‌طور ساده موضوع سوءفهمی در میان است. ما نباید سؤال‌های مختلف را با یکدیگر خلط کنیم؛ این سؤال‌ها به عقیده‌ی من به شیوه‌های مختلف مشاهده تعلق دارد، که در عین حال مکمل یکدیگر است. وقتی از آزادی اراده حرف می‌زنیم، منظور ما آن موقعیتی است که در آن باید تصمیمی بگیریم، این موقعیت، موقعیت دیگری را نفی می‌کند که در آن محرکات رفتار خود را تحلیل می‌کنیم یا حتی آن موقعیتی را نفی می‌کند که در آن فرایندهای فیزیولوژیکی را، مثلا فرایندهای الکتروشیمیایی مغز را مطالعه می‌کنیم. پس در اینجا با موقعیت‌هایی سرو کار داریم که نوعا کاملا مکمل یکدیگر است و به همین سبب هم این سؤال، که آیا قوانین طبیعی به قطع یا به احتمال تعیین کننده‌ی آن رویداد است، به سؤال آزادی اراده مستقیما مربوط نمی‌شود. مسلم است که این شیوه‌های مختلف مشاهده، باید سرانجام با یکدیگر سازگار باشد، یعنی اینکه باید بتوانیم آن‌ها را بی‌ابهام بشناسیم، چون همگی به واقعیتی یکسان تعلق دارد؛ اما اینکه در جزئیات هریک چه پیش می‌آید، چیزی است که عجالتا هنوز نمی‌دانیم و سرانجام وقتی حرف از مداخله‌ی خداست، از محدودیت علمی آن رویداد، به‌طور آشکار حرفی زده نمی‌شود، بلکه حرف از آن رابطه‌ی معنایی است، که آن رویداد را با رویدادهای دیگر یا با فکر انسان پیوند می‌دهد؛ اما این رابطه‌ی معنایی هم به امر واقع تعلق دارد، درست مثل آن محدودیت علمی و شاید هم ساده‌ انگاری کاملا به خطایی باشد که آن رابطه‌ی معنایی را فقط به حساب وجه ذهنی واقعیت بگذاریم، اما در اینجا هم می‌توان از موقعیت‌های شبیه به هم در علم درس گرفت. در زیست شناسی روابط شناخته شده‌ای وجود دارند، که بنابر کِنه‌شان عِلّی نیستند، بلکه غایی‌اند، یعنی بنا بر هدفی که دارند تشریح می‌شوند. می‌توان مثلا فرایند بهبود موجود زنده‌ای را در نظر گرفت که جراحی برداشته است. تفسیر غایت‌گرا، رابطه‌ی مکملی سنخی‌ای با آن تفسیری دارد، که براساس قوانین شناخته‌ شده‌ی فیزیکی- شیمیایی، با قوانین فیزیک اتمی صورت گرفته است، به این معنا که در یک مورد سؤال می‌کنیم که آیا فرایند، برای رسیدن به هدف دلخواهش، یعنی برقراری دوباره روابط عادی در موجود زنده، در خود ارگانیسم صورت می‌گیرد، یا آنکه در مورد دیگر، براساس جریان علّی پدیده‌های مولکولی است. این دو شیوه‌ی مشاهده یکدیگر را نفی می‌کنند، اما ضرورتا هم در تضاد با یکدیگر نیست. کاملا بجاست تا بپذیریم که بررسی قوانین مکانیک کوانتومی در ارگانیسم زنده، این قوانین را درست به همان اندازه تأیید می‌کند که در ماده بی جان، با این وجود، تشریح غایت‌گرا هم کاملا درست است. گمان می‌کنم که پیشرفت فیزیک اتمی به‌سادگی به ما آموخت، که باید از حالا به بعد با ظرافت بیشتری فکر کنیم.

گفتم:

ما باز هم، خیلی راحت‌تر از آنچه فکرش را می‌کردیم، به وجه معرفت شناختی دین برگشتیم، اما دفاعیه‌ی دیراک برضد دین هم به‌خصوص مربوط‌به وجه اخلاقی آن می‌شد، دیراک می‌خواست به‌خصوص از آن بی‌صداقتی یا خود فریبی‌ای انتقاد کند که خیلی هم راحت به هر فکر دینی می‌پیوندد و او هم به حق آن را تحمل نمی‌کرد. اما در اینجا خودش هم خردگرای متعصبی شده است، احساس من هم این است که در اینجا خردگرایی نمی‌تواند کافی باشد!

 نیلز گفت:

چقدر عالی شد که دیراک این قدر با حرارت به خطر خود فریبی و تضادهای درونی اشاره کرد، اما این هم کاملا لازم بود، که ولفگانگ با تذکرش که از سر شوخی بود، دست آخر او را متوجه کرد که چقدر دشوار است تا خودمان را از دست این خطر کاملا در امان نگاه داریم.

نیلز این گفت و گو را با یکی از آن قصه‌هایی تمام کرد، که در چنین وقت‌هایی بارغبت تعریف می‌کرد:

 در نزدیکی خانه‌ی ییلاقی ما در تیس‌ویل مردی زندگی می‌کند، که بالای در ورودی خانه‌اش نعل اسبی آویزانکرده است. این نعل اسب بنا بر روایت عامیانه کهنی خوشبختی می‌آورد آشنایی از او پرسیده بود راستی راستی، تو این قدر خرافاتی هستی؟ واقعا عقیده داری که این نعل اسب برای تو خوشبختی می‌آورد؟ مرد هم جواب داده بود؛ مسلما نه، اما می‌گویند که این نعل تازه وقتی اثر دارد، که به آن اعتقاد نداشته باشی!

پایان قسمت دوم

پیشنهاد می‌شود که پس از گذشت ۲۴ ساعت از مطالعه این بخش، اقدام به مطالعه‌ی بخش سوم و پایانی این مقاله کنید.

جمع تازه‌ی ما در لایپزیک در آن سال‌ها به سرعت گسترش می‌یافت. جوانانی با استعداد از کشورهای مختلف به سوی ما می‌آمدند، تا در پیشبرد مکانیک کوانتومی سهمی داشته باشند، یا آن را در مورد ساختار ماده به کار گیرند و این فیزیکدانان پرشور، با ذهن‌هایی که بر هر نوآوری‌ای گشوده بود، بحث‌های ما را در درس گروهی بارورتر می‌کردند و شاید هر ماه یک بار به گسترش فضایی می‌پرداختند، که می‌توانست اندیشه‌های نو را در بر گیرد. فلیکس بلوخ سویسی فهم از خواص الکتریکی فلزات را توضیح می‌داد، لانداو از روسیه و پایرلس درباره‌ی مسائل ریاضی الکترودینامیک کوانتومی حرف می‌زدند، فریدریش هوند نظریه‌ی پیوند شیمیایی را پیش می‌برد و ادوارد تلر هم خواص نوری مولکول‌ها را محاسبه می‌کرد. کارل فریدریش فون وایتسکر هم که هنوز هجده سال تمام نداشت، به این گروه پیوست و به بحث‌ها هم رنگی فلسفی می‌داد و اگرچه او در رشته فیزیک درس می‌خواند، کاملا می‌توانستیم دریابیم که هرگاه در آن درس‌های گروهی، مسائل فیزیکی، پرسش‌های فلسفی یا معرفت شناختی را بر می‌انگیخت، او با دقت و توجه به آن‌ها گوش می‌کرد و با دل و جان درباره‌ی آن‌ها بحث می‌کرد.

یک یا دو سال بعد، به‌ویژه فرصتی پیش آمد تا به گفتگوهای فلسفی بپردازیم و این درست زمانی بود که فیلسوفی جوان گرته هرمان، به لایپزیک آمد، تا با فیزیکدانان اتمی درباره‌ی ادعاهای فلسفی آن‌ها گفت‌وگو کند. هرمان از همان آغاز هم به نادرستی آن ادعاها یقین داشت. گرته هرمان در جمعی که به دور نلسون، فیلسوف اهل گوتینگن، گرد آمده بود، هم درس خوانده بود و هم با آن‌ها همکاری کرده بود. او در آنجا با جریان‌های فکری فلسفه‌ی کانت آشنا شده بود، بدان گونه که در آغاز قرن نوزدهم، فریس، فیلسوف و طبیعت شناس آن‌ها را تفسیر کرده بود. از خواسته‌های مکتب فریس و جمع نلسون هم یکی آن بود، که تفکرات فلسفی هم باید به میزان ریاضیات نوین استحکام می‌داشت. با این میزان از استحکام هم، گرته هرمان حالا می‌خواست نشان دهد، که در قانون علیت، آن‌گونه که کانت آن را ارائه کرده است، نمی‌توان دست برد، اما به عکس آنچه او گمان می‌کرد، مکانیک کوانتومی نوین به این شکل از قانون علیت از برخی از جهات تردیدهایی داشت. فیلسوف جوان ما اما مصمم بود تا این پیکار را تا پایان ادامه دهد.

در اولین جلسه‌ی بحث، با کارل فریدریش و با من، او شاید با طرح افکاری نزدیک به این مضمون آغاز کرده باشد؛

در فلسفه‌ی کانت، قانون علیت، ادعایی تجربی نیست که از راه تجربه بتوان آن را اثبات یا رد کرد، بلکه به عکس پیش شرطی بر هر تجربه‌ای است و به‌علاوه این قانون به مقولات فکری‌ای متعلق است، که کانت آن‌ها را ماتقدم می‌نامد. تأثیرات حسی‌ای، که ما جهان را با آن‌ها ادراک می‌کنیم، نمی‌تواند به‌گونه‌ای بازی‌ای ذهنی از آن احساس‌هایی باشد، که هیچ عینی متناظر با آن‌ها نیست، اگر هیچ قاعده‌ای وجود نداشته باشد که این تأثیرات در پی آن فرایندی بیاید که پیش‌تر دست اندرکار بوده است. بر این قاعده یعنی؛ پیوند روشن میان علت و معلول هم، اگر بخواهیم بدان ادراکات عینیت دهیم، یعنی اگر بخواهیم ادعا کنیم که خبری، بر چیزی یا فرایندی یافته‌ایم، باید پیش شرطی بنهیم. اما علم هم، از طرف دیگر با تجربه سر و کار دارد و در اینجا هم به‌ویژه با تجربیات عینی تنها آن تجربیاتی که دیگران هم بتوانند درستی آن‌ها را بیازمایند و این تجربیات، که به این معنای دقیق عینی است، می‌تواند موضوع علم باشد و از اینجا ناگزیر این نتیجه به دست می‌آید که همه‌ی علم باید قانون علیت را پیش شرطی بر خود بنهد و تا زمانی هم که علم هست، قانون علیت هم خواهد بود. قانون علیت تا حدودی ابزار فکری ما می‌ماند، که با آن می‌کوشیم تا مصالح خام دریافت‌های حسی خود را با آن به شکل تجربه در آوریم و تا آنجا که این کار در حدی بر ما میسر شود، موضوعی هم برای علم در اختیار داریم. پس چگونه ممکن است که مکانیک کوانتومی هم بخواهد قانون علیت را سست کند و هم در عین حال علم باقی بماند؟

اما من هم در اینجا ناگزیر شدم تا به تجربیاتی اشاره کنم که به تفسیر آماری مکانیک کوانتومی انجامید؛

فرض کنیم که با اتمی منفرد از نوع رادیوم B سرو کار داریم. حقیقت این است که این کار آسان‌تر است تا با تعداد بیشتری از این اتم‌ها به تجربه بپردازیم، یعنی با مقدار کمی از رادیوم B به‌جای یک اتم. اما از نظر اصولی هم هیچ اشکالی وجود ندارد تا رفتار یک اتم از این نوع را بررسی کنیم. اما این را هم می‌دانیم که دیر یا زود اتم رادیوم B در جهتی الکترونی گسیل می‌کند و به اتم رادیوم C تبدیل می‌شود. به‌طور میانگین کمتر از نیم ساعت طول می‌کشد تا این کار روی دهد. اما این کار ممکن است پس از چند ثانیه یا پس از چند روز اتفاق بیفتد. به‌طور میانگین به این معنا است که وقتی با تعداد زیادی از اتم‌های رادیوم B سرو کار داریم، پس از نیم ساعت تقریبا نصف آن تبدیل شده است. اما در اینجا نمی‌توانیم در مورد یک اتم منفرد رادیوم B علتی را برشمریم، که چرا این اتم اکنون و نه پیش‌تر یا دیرتر تبدیل شده است، یا آن که چرا در این جهت و نه در جهتی دیگر الکترونی گسیل کرده است و این خود نشانی بر آن است، که قانون علیت تا حدودی ناکارآمد بوده است و ما هم به دلایل زیادی بر این نکته یقین داریم که چنین علتی وجود ندارد.

گرته هرمان هم پاسخ داد:

بله، از قضا اشتباه فیزیک اتمی هم شاید در همین‌جا باشد. در پی این واقعیت که ما برای رویداد معینی هنوز علتی نیافته‌ایم، نمی‌توان به هیچ وجه این نتیجه را گرفت که علتی هم وجود ندارد. من می‌توانم تنها از آن این چنین نتیجه بگیرم، که هنوز مسئله‌ای حل نشده پیش روی ماست، یعنی اینکه فیزیکدانان باید بازهم بکاوند، تا علت آن را بیایند، خبری که ما از اتم رادیوم B پیش از گسیل الکترون داریم، به‌طور آشکار هنوز ناقص است، زیرا که در غیر این صورت می‌توانستیم معین کنیم که چه وقت و در چه جهتی الکترون گسیل می‌شود. پس باید بیشتر بکاویم تا به اطلاعی کامل دست یابیم.

من هم کوشیدم تا بیشتر توضیح دهم؛

خیر، اطلاع ما در این‌باره کامل است، زیرا که از دیگر تجربیاتی که ما با این اتم رادیوم B می‌توانیم انجام دهیم، این نتیجه برمی‌آید که اجزای مشخص کننده دیگری بر این اتم وجود ندارد، جز آن که پیش از این می‌شناختیم. بهتر است اما روشن‌تر بگویم؛ بر ما اکنون این نکته روشن شده است، که نمی‌دانیم الکترون در چه سمتی گسیل می‌شود و شما هم در این مورد پاسخ دادید که باید بیشتر آن اجزای مشخص کننده را بکاویم تا بتوانیم آن سمت را معین کنیم. اما حالا باز هم فرض کنیم، که ما آن اجزای مشخص‌کننده را یافته باشیم، با این کار هم دوباره با مشکل دیگری رودررو می‌شویم، الکترون گسیل شده را می‌توانیم موجی مادی در نظر بگیریم، که از هسته‌ی اتم تابیده می‌شود. این چنین موجی هم اما می‌تواند سبب بروز پدیده تداخل شود و باز هم فرض کنیم که بخشی از موجی که از هسته‌ی اتم در جهت مخالف تابیده می‌شود به دستگاهی که به همین منظور قرار داده‌ایم وارد شود، که سبب بروز تداخل شود که در نتیجه‌ی آن خاموشی در جهت معینی از دستگاه پدیدار می‌شود. این کار به این معنی خواهد بود، که با قطعیت می‌توانیم پیش‌بینی کنیم، که الکترون سرانجام در این جهت تابیده نشده است. اما اگر اجزای مشخص کننده تازه‌ای را شناخته بودیم، از آن‌ها چنین نتیجه می‌شد که الکترون از این پس از هسته در جهت معینی گسیل می‌شود، به طوری که دیگر پدیده‌ی تداخل بروز نمی‌کند، خاموشی هم دیگر در اثر تداخل پدیدار نمی‌شود و آن نتیجه هم استوار نمی‌ماند. حقیقت این است که خاموشی را در تجربه هم می‌توانیم مشاهده کنیم. پس طبیعت به ما می‌آموزد که آن اجزای مشخص کننده‌ی مورد نزاع اصلا وجود ندارد و اطلاع ما هم‌اکنون هم بدون آن اجرای مشخص کننده کامل است.

گرته هرمان هم در جواب گفت:

 اما این هم وضع خیلی بدی است. شما از طرفی هم می‌گویید، که اطلاع ما از اتم رادیوم B ناقص است، زیرا که نمی‌دانیم که چه وقت و در چه جهت الکترون گسیل می‌شود؛ اما از طرف دیگر هم می‌گویید که اطلاع ما کامل است، زیرا که اگر اجزای مشخص کننده‌ی دیگری وجود داشت، ما در برخی دیگر از تجربه‌ها به تناقض برخورد می‌کردیم. اما اطلاع ما نمی‌تواند هم کامل باشد و هم ناقص، حقیقتا این اتفاق کاملا بی معنی است!

کارل فریدریش هم وارد این بحث شد، تا پیش شرط‌های فلسفه کانت را دقیق‌تر تحلیل کند؛

 این تناقض ظاهری که اینجا با آن رو در رو هستیم به این سبب پدیدار شده است، که ما درباره آنچه از آن حرف می‌زنیم، طوری رفتار می‌کنیم که گویا از اتم رادیوم B فی نفسه می‌توان حرف زد، اما این امر به هیچ وجه نه مسلم است و نه درست. حتی در نزد خود کانت هم چیز فی نفسه مفهومی مشکل است. کانت می‌دانست که درباره‌ی چیز فی نفسه نمی‌توان چیزی گفت؛ آنچه هست تنها اعیان ادراک است، اما فرض کانت هم این است که اعیان ادراک را می‌توانیم براساس نمونه‌ی چیز فی نفسه به یکدیگر پیوند دهیم یا منظم کنیم. پس او بدین ترتیب آن ساختاری از تجربه را به‌عنوان ماتقّدم پیش شرط می‌داند، که ما در زندگی روزانه بدان عادت کرده‌ایم و اینکه آن‌ها در شکلی دقیق‌تر بنیاد فیزیک کلاسیک را می‌نهند. براساس این نظر، جهان از چیزهایی در فضا درست شده است که در زمان تغییر می‌کند، از فرایندهایی تشکیل شده است که براساس قاعده‌ای در پی یکدیگر می‌آید، اما ما در فیزیک اتمی آموخته‌ایم، که ادراکات ما دیگر براساس نمونه‌ی چیز فی نفسه به یکدیگر نمی‌پیوندد، یا آنکه دیگر نمی‌توان آن‌ها را بر آن اساس منظم کرد. به همین سبب هم اتم رادیوم B، فی نفسه وجود ندارد.

گرته هرمان حرف کارل فریدریش را قطع کرد و گفت:

آن طور که شما مفهوم چیز فی نفسه را به کار می‌گیرید، به گمانم به‌طور دقیق با روح فلسفه کانت نمی‌خواند. شما باید میان چیز فی نفسه و موضوع فیزیکی آن به روشنی فرق نهید. چیز فی نفسه در نظر کانت پدیدار نمی‌شود، حتی به‌صورت غیر مستقیم!

این مفهوم در علم و در تمام فلسفه‌ی نظری تنها کارش این است، که آن چیزی را بنمایاند، که درباره آن مطلقا هیچ چیز نمی‌توانیم بدانیم؛ زیرا که همه‌ی اطلاع ما وابسته به تجربه است و تجربه هم بدین معنی است که چیزها را آن‌گونه بشناسیم که بر ما پدیدار می‌شود. حتی شناخت هم به‌طور ماتقدم به چیزها نمی‌پردازد، آن‌گونه که آن‌ها می‌خواهند باشند، بلکه تنها کارش این است که تجربه را ممکن کند. اما وقتی که شما به معنای فیزیک کلاسیک از اتم رادیوم B فی نفسه حرف می‌زنید، بیشتر منظورتان چیزی است که کانت آن را عِین یا موضوع می‌نامد. عین بخشی از جهان پدیدار است، مانند میز و صندلی، ستاره و اتم!

کارل پرسید:

حتی وقتی که آن‌ها را نمی‌توان دید، مثلا اتم را؟

و هرمان چنین پاسخ داد؛

حتی در آن وقت، زیرا ما آن‌ها را از پدیدار نتیجه می‌گیریم. جهان پدیدار چارچوبی منسجم دارد و حتی در ادراک روزمره هم ممکن نیست، تا به روشنی میان آنچه می‌توانیم مستقیم ببینیم و آنچه می‌توانیم استنتاج کنیم، فرقی بنهیم. شما این صندلی را می‌بینید، اما پشت آن را در همین لحظه هم نمی‌توانید ببینید؛ اما شما با همان یقینی که به روی صندلی دارید و آن را می بینید، پشت آن را هم می پذیرید و این بدین معنی است که علم عینی است؛ علم به این سبب عینی است، که شما از ادراکات حرف نمی‌زنید، بلکه از اعیان می‌گویید!

کارل گفت:

اما اتم چیزی است، که ما نه روی آن را می‌توانیم ببینیم و نه پشت آن را. پس چه دلیلی دارد که آن هم همان ویژگی‌های میز و صندلی را داشته باشد؟

گرته در مقام پاسخگویی برآمد؛

زیرا که اتم هم عین است. بدون عین نمی‌تواند علمی عینی وجود داشته باشد و اینکه عین چه چیز است، از راه مقولاتی نظیر جوهر و علیت و مانند آن‌ها معین می‌شود. اگر شما از به کارگیری دقیق این مقولات چشم پوشی کنید، با این کار اصلا از امکان تجربه هم صرف‌نظر کرده‌اید.

کارل فریدریش اما دیگر نمی‌خواست بحث را سست کند؛

در نظریه‌ی کوانتومی حرف از شیوه‌ای نو است، تا به ادراکات عینیت دهیم و این آن چیزی است که کانت نمی‌توانست در آن زمان بدان رسیده باشد. هر ادراکی به یک وضع مشاهده باز می‌گردد، که باید مشخص باشد، حتی اگر ادراک تجربه را در پی داشته باشد. حاصل ادراکات نمی‌تواند به همان شیوه، که در فیزیک کلاسیک ممکن بود، عینیت بیابد. وقتی تجربه‌ای انجام شده است، از آن می‌توان نتیجه گرفت که در اینجا هم‌اکنون رادیوم B موجود است؛ پس در این وضع مشاهده این خبر کامل است. اما در وضع مشاهده‌ی دیگری که باید اخباری درباره‌ی گسیل الکترون بدهد، این خبر دیگر کامل نیست. وقتی دو وضع مشاهده‌ی مختلف با یکدیگر مرتبط است، آن چنان که بور آن‌ها را مکمل یکدیگر می‌داند، این بدان معنی است که اطلاعی کامل از یکی در وضعی از مشاهده، در عین حال اطلاعی ناقص در مورد دیگری است.

گرته با لحنی خاص چنین جواب داد؛

 و به این ترتیب می‌خواهید تحلیل کانت از تجربه را یکسره ویران کنید؟

کارل گفت:

نه و به نظر من هم اصلا چنین چیزی ممکن نیست. کانت خود به درستی دریافته بود، که چگونه می‌توان تجربه را به دست آورد و من هم یقین دارم که تحلیل کانت در اصول آن درست است. اما آنجا که کانت صور ادراک از فضا و زمان و مقوله‌ی علیت را ماتقدم بر تجربه می‌داند، در آنجا این خطر را به جان می‌خرد، که آن‌ها را در عین‌حال هم مطلق بگمارد و هم مدعی شود که آن‌ها از نظر محتوایی هم باید در هر نظریه‌ی فیزیکی دلخواه پدیدارها به یک صورت ظاهر شود. اما آن چنان که نظریه‌ی نسبیت و نظریه‌ی کوانتومی نشان داده است، وضع این چنین نیست. اما در یک مورد باز هم حق کاملا با کانت است؛ تجربه‌هایی که فیزیکدان به آن‌ها دست می‌زند، باید همواره به زبان فیزیک کلاسیک تشریح شود، زیرا که به‌صورت دیگر هرگز ممکن نیست تا بتواند فیزیکدان دیگری را از آن چیزی مطلع کند، که آن را پیمایش کرده است و از این راه دیگری را در وضعی قرار می‌دهیم تا بتواند آن نتایج را وارسی کند. ماتقدم کانت از فیزیک جدید به هیچ وجه زدوده نشده است، اما به شیوه‌ای هم نسبی شده است. مفاهیم فیزیک کلاسیک، یعنی مفاهیم فضا، زمان و علیت هم به این معنا بر نظریه‌ی نسبیت و نظریه‌ی کوانتومی ماتقدم است، زیرا که آن‌ها را در تشریح تجربیات باید به کار گیریم و برای آن که با احتیاط بیشتری حرف بزنیم، می‌گوییم که زیرا آن‌ها را درواقع باید به کار گیریم، اما همین مفاهیم در نظریات جدید از نظر محتوایی تعدیل شده است.

گرته هرمان گفت:

با همه‌ی آنچه گفتید، هنوز پاسخ روشنی بر پرسش آغازین خود نیافتم. من می‌خواستم، بدانم که چرا ما در آنجا علتی نیافتیم، که بر پیش‌بینی‌ ما از رویدادی، مثلا از گسیل الکترون، کفایت کند تا ناگزیر به کاوش بیشتر نباشیم. مسلما شما نمی‌خواهید ما را از کاویدن باز دارید، اما در عین حال هم می‌گویید که این کاوش به جایی نمی‌انجامد، زیرا که اجزای مشخص کننده دیگری وجود ندارد، آنچه را به‌طور دقیق عدم قطعیت از راه ریاضی بیان می‌کند، سبب می‌شود تا برای آرایش تجربی دیگری جایی باقی گذارد، تا به پیش‌بینی مشخص دیگری بینجامد و این امر را هم تجربه تأیید می‌کند و با این طور حرف زدن به نظر می‌رسد، که عدم قطعیت به نحوی واقعیتی فیزیکی است، که خصلتی عینی می‌یابد، درحالی‌که به‌طور معمول عدم قطعیت به معنای بی‌اطلاعی تفسیر می‌شود و به این سبب هم ذهنی محض است.

اینجا بود که دوباره در آن گفت‌وگو مداخله کردم و گفتم:

با این کار شما خصلت شاخص نظریه‌ی کوانتومی امروزی را بر شمردید. هرگاه بخواهیم از پدیده‌های اتمی قانونمندی‌هایی را نتیجه بگیریم، کار به اینجا می‌رسد که دیگر نمی‌توانیم فرایندهای عینی را در فضا و زمان براساس قاعده‌ای به یکدیگر بپیوندیم، بلکه می‌توانیم، اگر بخواهیم اصطلاحی دیگر را از روی احتیاط به کار گیریم، وضع مشاهده‌های مختلف را به یکدیگر مرتبط کنیم. اما در اینجا هم چیزی که عایدمان می‌شود، قانونمندی‌های تجربی است. نمادهای ریاضی که به کمک آن‌ها این وضع مشاهده را تشریح می‌کنیم، بیشتر ممکن را دربرابر واقع می‌نمایاند. شاید بتوان گفت که آن‌ها چیزی میان ممکن و واقع را می‌نمایانند، که در مورد آن عینی در بهترین صورت به همان معنایی به کار برده می‌شود، که در نظریه‌ی آماری حرارت درباره‌ی دما گفته می‌شود. این شناخت مشخص از ممکن، هر چند پیش‌بینی‌های دقیق و مطمئن را مجاز می‌شمرد، اما علی‌القاعده تنها این امکان را می‌دهد تا درباره‌ی رویدادی آتی، نتایجی درباره‌ی احتمال وقوع آن را استخراج کنیم. کانت نمی‌توانست پیش‌بینی کند، که در حوزه‌های تجربی، که بسیار هم فراتر از تجربیات روزانه ما می‌رود، دیگر نمی‌توان نظامی را به کار برد که مدرک را براساس نمونه‌ی چیز فی نفسه، یا بهتر بگوییم براساس موضوع منظم کند و برای آنکه آن را به زبان ساده‌تری بیان کنیم، اتم دیگر نه چیز است و نه موضوع!

هرمان پرسید:

پس اتم بالاخره چیست؟

پاسخ دادم؛

برای این پرسش هیچ لفظی در زبان وجود ندارد، زیرا که زبان ما براساس تجربه‌ی روزانه ما ساخته می‌شود و اتم هم از قضا موضوع تجربه‌ی روزانه ما نیست. اما اگر به شکل دیگری از بیان رضایت دهید، می‌گویم که، اتم جزء سازنده‌ی وضع مشاهده است، این جزء سازنده در تحلیل فیزیکی پدیده‌ها ارزش تبیینی بسیار دارد.

کارل فریدریش دوباره گفت:

وقتی از مشکلات درباره‌ی الفاظ در زبان حرف می‌زنیم، شاید بهترین درسی که می‌توانیم از فیزیک نوین بیاموزیم این باشد، که همه مفاهیمی که با آن‌ها به تشریح تجربیات خود می‌پردازیم، حوزه کاربردی محدودی دارد. با همه این مفاهیم مانند؛ چیز، عین ادراک، لحظه‌ی زمانی، هم‌زمانی، امتداد و مانند این‌ها می‌توانیم وضعیت‌های تجربی‌ای را نشان دهیم، که در آن‌ها با این مفاهیم با اشکال رو‌به‌رو شده‌ایم. اما این هم بدین معنی نیست که این مفاهیم در عین حال هم پیش شرطی بر هر تجربه‌ای نباشد، بلکه به این معنی است که موضوع پیش شرطی مطرح است، که هر چند باید بدان منتقدانه نگریست، اما از آن هم نمی‌توان توقع مطلق داشت.

گرته هرمان از اینکه بحثمان به اینجا رسیده بود، خیلی هم خوشحال نبود، هرمان امید داشت تا بتواند با ابزارهای فکری فلسفه‌ی کانت تمام ادعاهای فیزیکدانان اتمی را با حدّت رد کند، یا به عکس این نکته را دریابد که شاید کانت در جایی مرتکب اشتباه فکری مهمی شده باشد، اما به ناگاه چنین به نظرش رسید که بازی‌ای با نتیجه‌ی مساوی در جریان است، که در آن میان آرزویش به رسیدن به روشنی هم چندان برآورده نشده است. به همین سبب دوباره پرسید:

راستی آیا این نسبی انگاشتن ماتقدم کانت، حتی در زمان به معنای نومیدی بی‌چون و چرا نیست، که بگویم ما اصلا هیچ چیز نمی‌توانیم بدانیم؟ و به راستی به نظر شما هیچ جایی در شناخت وجود ندارد، که در آنجا بتوانیم استوار بایستیم؟

کارل فریدریش با چالاکی پاسخ داد، که از قضا سیر علم این امید را در ما بیدار می‌کند تا نظری با خوش بینی بیشتری داشته باشیم؛

وقتی می‌گوییم که کانت با ماتقدم خود، وضع شناخت از علم در گذشته را به درستی تحلیل کرده است، اما ما امروز در فیزیک اتمی با وضع جدیدی از شناخت رودررو هستیم، شاید این خبر اندک نزدیکی‌ای با خبر دیگری داشته باشد، که بگوییم قانون اهرم‌های ارشمیدس، که برای فناوری زمان خود مهم‌ترین قواعد عملی به حساب می‌آمده است، بهترین بیان عملی بوده است، اما این قوانین امروز برای فناوری، برای مثال در الکترونیک، دیگر کافی نیست. قانون اهرم‌های ارشمیدس دانش محض است و نه نظری آمیخته به ابهام! این قوانین برای همه‌ی زمان‌ها درست است، هر گاه که حرف از اهرم باشد و اگر روی سیاره‌ی دیگری، جایی در آن دور دست‌ها، در منظومه ستارگان اهرمی یافت شود، در آنجا هم ادعای ارشمیدس درست است. بخش دوم این خبر که بشر با پیشرفت دانش در حوزه‌ی فناوری به پیش رفته است، به طوری که دیگر مفهوم اهرم کافی نیست، درواقع نه به معنای نسبی کردن است و نه به معنای تاریخی انگاشتن قوانین اهرم‌ها. این خبر تنها به این معنا است که قوانین اهرم‌ها در تکامل تاریخی خود بخش‌هایی از نظام فنی جامع‌تری شده است که در آن، این قوانین دیگر آن اهمیت اساسی را که در آغاز داشت، ندارد، درست به همین دلیل یقین دارم که تحلیل کانت از شناخت، دانش محض است، که نه‌تنها نظری آمیخته به ابهام نیست، بلکه آن تحلیل همواره تا زمانی‌که موجوداتی زنده وجود دارند که می‌توانند بیاندیشند، که می‌توانند در پیرامون خود با یکدیگر رابطه داشته باشند، تا آنچه ما از دیدگاه خود تجربه می‌نامیم، پدیدار شود، درست باقی می‌ماند، اما ماتقدم کانت هم می‌تواند روزی از جایگاه مرکزی خود بیرون رانده شود و بخشی از تحلیلی بسیار جامع‌تر از فرایند شناخت شود و این به یقین نادرست است، که بخواهیم از ارزش دانش علمی یا فلسفی آن با این حکم که هر عصری حقیقت خاص خود را دارد، بکاهیم، اما این نکته را هم باید در نظر داشته باشیم، که با تکامل تاریخی، حتی ساختار فکر بشری هم دگرگون می‌شود، پیشرفت علم تنها در این نیست، که بر ما واقعیاتی نو آشکار می‌کند، که ما فهم می‌کنیم، بلکه در این هم هست که ما همواره چیزهایی نو می‌آموزیم، که از معنای کلمه فهمیدن بر می‌خیزد.

با این پاسخ، که بخشی از آن، گفته‌ی بور بود، گرته هرمان به گمان ما اندکی خشنودتر به نظر می‌رسید. ما همچنین احساس می‌کردیم که رابطه‌ی فلسفه کانت با علوم جدید را بهتر فهمیده‌ایم!