الگوریتم یونان باستان اعداد اول را شناسایی میکند

ریاضیدانهای زیادی با موضوع اعداد اول دچار مشکل شدهاند! همان اعدادی که "اتم"های دنیای ریاضی به شمار میآیند و جز بر خودشان و عدد یک بر هیچ رقم دیگری بخشپذیر نیستند.
افراد زیادی برای پیدا کردن اعداد اول دست به کار شدند و با پشتکار (و حتی انگیزههای مالی) به دنبال محاسبهی اعداد اول بزرگتر پرداختند. با این حال یکی از ریاضیدانهای مطرح دنیا، کلید حل معما را در یکی از الگوریتمهای یونان باستان به نام "غربال اراتوستن" کشف کرده است.
غربال اراتوستن، همان طور که از نامش پیدا است، یک غربال ریاضی است که کمک میکند تا اعداد اول از بین دیگر اعداد فیلتر شوند.
حدود ۲۴۰ سال قبل از میلاد مسیح، ستارهشناس و ریاضیدان یونانی به نام "سایرن" (Cyrene) این الگوریتم را بسط داد تا افراد بتوانند اعداد اول واقع در یک محدودهی عددی مشخص را پیدا کنند.
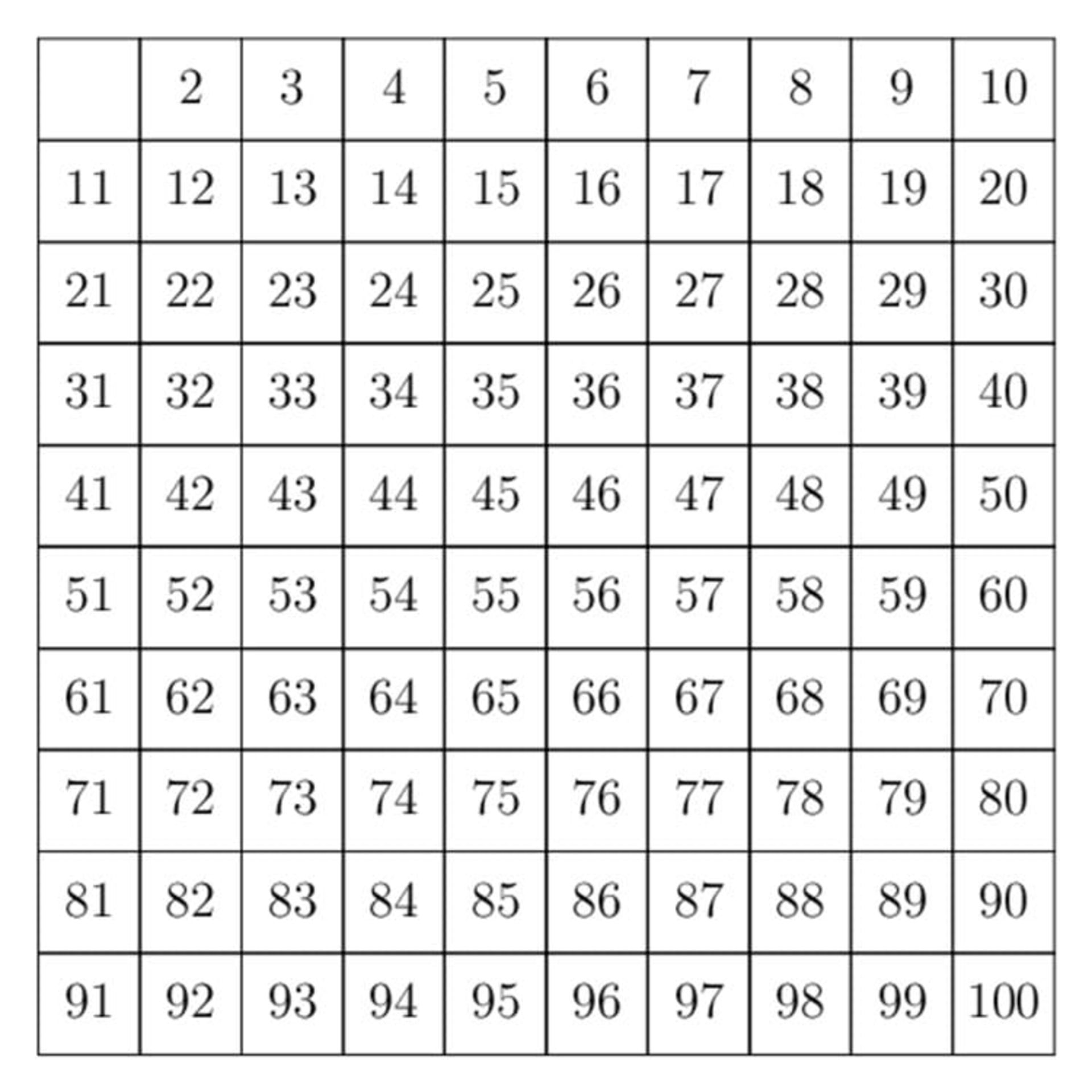
روند کار به این شکل است که ترتیبی از اعداد (برای مثال ۱ تا ۱۰۰) را روی یک تکه کاغذ مینویسید. ابتدا اعداد مضرب ۲ را (به غیر از ۲) حذف میکنید. سپس به حذف اعداد مضرب ۳ (به غیر از ۳) میپردازید و این روند را برای اعداد بعد هم تکرار میکنید. هر عددی که در برگهی چرکنویس شما جان سالم به در برد، در دستهی اعداد اول قرار میگیرد.
البته این روش در مورد محدودههای وسیع اعداد کارآیی چندانی ندارد. (آخرین عدد اول کشف شده دارای ۲۲ میلیون رقم است). با این حال غربال اراتوستن میتواند به یک الگوریتم قابل اجرا در کامپیوتر تبدیل شود. مشکل بزرگی که در ارتباط با این الگوریتم وجود دارد این است که حجم زیادی از حافظهی سیستم را درگیر میکند و همین امر استفاده از این روش را برای ریاضیدانهای امروزی ناکارآمد جلوه میدهد.

در حال حاضر، یک ریاضیدان ردهبالا به نام "هارالد هلفگات" (Harald Helfgott) یک راهکار ساده برای به کارگیری الگورتیم اراتوستن پیدا کرده است و احتمال میدهد که این روش بتواند در آینده کلید کشف اعداد اول باشد.
هلفگات یک ریاضیدان پرویی فعال در مرکز ملی تحقیقات علمی فرانسه ودانشگاه "گوتینگن" (Göttingen) آلمان است. وی شهرت خود را در سال ۲۰۱۳ پس از حل مسئلهای به دست آورد که ۲۷۱ سال بیپاسخ مانده بود. اکنون، هلفگات موفق شده است تا با تکنیکی به نام "روش دایره" (circle method) نسخهای بهبود یافته از غربال اراتوستن ارایه دهد تا حجم کمتری از حافظهی کامپیوتر را درگیر کند.
چند تن از ریاضیدانها در خصوص این بهینه سازی میگویند:
فرض کنید که یک کامپیوتر هستید که حافظهی شما، این اطلاعات را به صورت دادههای ثبت شده در کاغذ ذخیره میکند. چنانچه بخواهید اعداد اول بین ۱ تا ۱۰۰۰/۰۰۰ را با استفاده از شکل اصلی الگوریتم به دست آورید نیاز به ۱۰/۰۰۰ ورق کاغذ خواهید داشت. حال آن که الگوریتم پیشنهادی هلفگات این رقم را به ۱۰۰ عدد میرساند.
البته این فشردهسازی تا حدی سرعت پردازش را کاهش میدهد اما هلفگات عقیده دارد که کامپیوترها با استفاده از حافظهی کش توانستند این مورد را جبران کنند.
به غیر از روش هلفگات، تکنیکها و الگوریتمهای دیگری وجود دارند که بتوانند اعداد اول را شناسایی کنند، اما آنچه این روش را متمایز میکند، امکان اجرای عملیاتی چون تجزیه و اتحاد است که اساس "رمزگذاری مدرن" به حساب میآید.
این احتمال وجود دارد که این روش بتواند تبدیل به ابزاری برای شناسایی یک عدد اول جدید شود. به هر حال، جایزهی ۱۵۰/۰۰۰ دلاری برای کسی که بتواند اولین عدد اول ۱۰۰ میلیون رقمی را پیدا کند، انگیزهای قوی به شمار میآید!
نظرات