
سختترین مسائل ریاضی حل نشده؛ از فرضیه ریمان تا P درمقابل NP
- سختترین مسائل ریاضی حل نشده
- مسئله جداسازی جداکننده (Separatrix Separation)
- حرکت براونی
- قضایای ناممکن
- مسئله مربع محاط شده
- فرضیه پیوستار
- استراتژی بهینه شطرنج
- مسائل ریاضی حلنشده که آسان بهنظر میرسند
- حدس اعداد اول دوقلو
- مسئله حرکتدادن مبل
- حدس کولاتز
- حدس بیل
- حدس گلدباخ
- مسائل ریاضی حل نشده جایزهدار (مسائل جایزه هزاره)
- فرضیه ریمان
- مسئله P درمقابل NP
- حدس هاج
- نظریه یانگ-میلز
- معادلات ناویه–استوکس
- حدس برش و سوینرتون-دایر
- جمعبندی
- سؤالات متداول
- مهمترین مسئله ریاضی حل نشده کدام است؟
- مسائل جایزه هزاره کدامند؟
- مسئله P درمقابل NP چیست؟
بگذارید از همین ابتدا با خودمان روراست باشیم؛ ریاضی واقعاً سخت است! آنقدر سخت که فهرست مسئلههای حلنشده در ریاضیات در ویکیپدیا بهطرز حیرتانگیزی طولانی و سرسامآور است. برخی از این مسائل قرنها است حلنشده باقی ماندهاند، هرچند باهوشترین افراد دنیا همواره مشغول پیداکردن راهی برای حلشان بودهاند؛ مثلاً مسئلهی حدس عدد تام فرد بیش از دو هزار سال پیش مطرح شده و یکی از کهنترین مسائل ریاضی حل نشده بهشمار میرود.
با وجود این دشواریها، اتفاقات هیجانانگیزی هر لحظه در دنیای ریاضیات و فیزیک در حال وقوع است؛ از هایپرگرافها و استفاده از آنها برای حل مسئله ریاضی ۵۰ ساله گرفته تا رازهای حل نشده بزرگ علم فیزیک و کشف راهحلی دقیق برای مسئله ریاضی سادهای که بیش از ۲۷۰ سال حلنشده باقی مانده بود.
در این مقاله، برخی از مهمترین و مشهورترین مسايل ریاضی حلنشده را در سه بخش سختترین مسائل، مسائلی که بهظاهر ساده میآیند و مسائل یک میلیون دلاری دستهبندی کردهایم تا با هم نگاهی گذرا به این دنیای پر رمزوراز داشته باشیم.
سختترین مسائل ریاضی حل نشده
سختترین مسئله ریاضی در دنیا چیست؟ راستش را بخواهید، جواب این سؤال پیچیده است؛ چون سطح «دشواری» برای افراد مختلف با مهارتهای مختلف، متفاوت است. برخی از مسائل ریاضی مثل سؤال ۶ المپیاد ریاضی سال ۱۹۸۸ فهمشان آسان است؛ اما حل کردنشان بهشدت دشوار.
این سؤال آنقدر سخت بود که حتی مسئولان المپیاد هم نتوانستند آن را در کمتر از شش ساعت حل کنند (جالب است بدانید ترنس تائو، برنده مدال فیلدز ۲۰۰۶ از هفت امتياز این سؤال، تنها یک امتیاز به دست آورد. البته او آن زمان فقط ۱۳ سالش بود.) برخی سوالات دیگر نیز مانند مسئله هفت پل کونیگسبرگ (Seven Bridges of Königsberg) به نظر پیچیده میآیند؛ اما راهحل آسانی دارند.
شاید بهترین معیار برای سنجش درجهی سختی مسائل ریاضی تعداد افرادی باشد که توانستهاند آن را حل کنند. بدینترتیب، سختترین مسائل ریاضی در دنیا آنهایی است که هنوز هیچ ریاضیدانانی موفق به حلشان نشده است. ازاینرو، هر شش مسئله جایزه هزاره که در انتهای مقاله با آنها آشنا خواهید شد و برای حلکردن هر کدام از آنها، یک میلیون دلار جایزه در نظر گرفته شده است، جزو سختترین مسائل ریاضی هستند. علاوهبراین شش مورد، صدها مسئله حلنشده دشوار دیگر نیز وجود دارد که اگرچه جایزهدار نیستند، به اندازهی مسايل جایزه هزاره میتوانند در پیشرفت علوم ریاضی تأثیرگذار باشند. در ادامه به معرفی برخی از آنها خواهیم پرداخت.
مسئله جداسازی جداکننده (Separatrix Separation)

یک آونگ در حال نوسان میتواند از یک طرف به طرف دیگر نوسان کند یا بهصورت یک دایره پیوسته دور خود بچرخد. نقطهای که آونگ از یک نوع حرکت به نوع دیگر میرسد، Separatrix (جداکننده) نامیده میشود و میتوان آن را در اکثر موقعیتهای ساده، محاسبه کرد. اما در شرایطی که آونگ با سرعت تقریباً ثابتی پیش میرود، دیگر هیچ راهحل ریاضی برای آن وجود ندارد. آیا معادلهای وجود دارد که بتواند این نوع separatrix را توصیف کند؟
حرکت براونی

پخششدن عطری را در یک اتاق تصور کنید. حرکت هر مولکول عطر طبق فرایندی موسوم به حرکت براونی (Brownian motion) تصادفی است؛ اما نحوه کلی حرکت گاز قابل پیشبینی است.
حرکت براونی در فیزیک به حرکت تصادفی ذرات غوطهور در مایع یا گاز بر اثر برخورد این ذرات با اتمها یا مولکولهای سیال گفته میشود. این پدیده به افتخار رابرت براون در سال ۱۸۲۷ نامگذاری شد، هرچند رابط ریاضی آن توسط آلبرت اینشتین در سال ۱۹۰۵ کشف و بدینترتیب گام نهایی در مورد پذیرش نظریه اتمی ماده و وجود اتمها و مولکولها برداشته شد.
حرکت براونی را میتوان بهلطف نظریه اینشتین با زبان ریاضی توصیف کرد؛ اما این توصیف صددرصد کامل نیست. براساس این نظریه، اگر بخواهیم به راهحل درست برسیم، مجبوریم قوانین آن را زیر پا بگذاریم؛ اما اگر بخواهیم به قوانین پایبند باشیم، هرگز به پاسخ دقیق نخواهیم رسید. آیا میتوان زبان ریاضی دیگری برای این پدیده تعریف کرد که هم به قوانین آن پایبند باشیم و هم به پاسخ دقیق برسیم؟ این همان چیزی است که مسئله نماها و ابعاد در پی حل آن است.
البته مشکل حرکت براونی تاحدی حل شده است. در سال ۲۰۰۰، گرگوری لاولر، اودد شرام و وندلین ورنر ثابت کردند که میتوان راهحلهای دقیقی برای دو مسئله در حرکت براونی بدون نقض قوانین آن پیدا کرد. این اثبات برای این سه دانشمند مدال فیلدز به ارمغان آورد که معادل جایزه نوبل است. استانیسلاو اسمیرنوف از دانشگاه ژنو نیز موفق به حل مسئلهی مرتبطی با حرکت براونی پدیده شد که او نیز بهخاطر این کشف مدال فیلدز دریافت کرد.
قضایای ناممکن
در دنیای ریاضی، مسائل زیادی وجود دارد که به نظر میرسد راهحلی ندارند. مثلاً عدد پی را در نظر بگیرید که نسبت محیط دایره به قطر آن است. زمانی که دانشمندان ثابت کردند در نظر گرفتن پایانی برای رقمهای پس از اعشار پی ناممکن است و این اعشار تا بینهایت ادامه دارد، کمک بسیار بزرگی به ریاضیات کرد.
به همین ترتیب، فیزیکدانان میگویند یافتن راهحل برای برخی مسائل از جمله اندازهگیری دقیق انرژی الکترونهایی که به دور اتم هلیوم میچرخند، ناممکن است. اما آیا میتوانیم این ناممکن را اثبات کنیم؟
مسئله مربع محاط شده
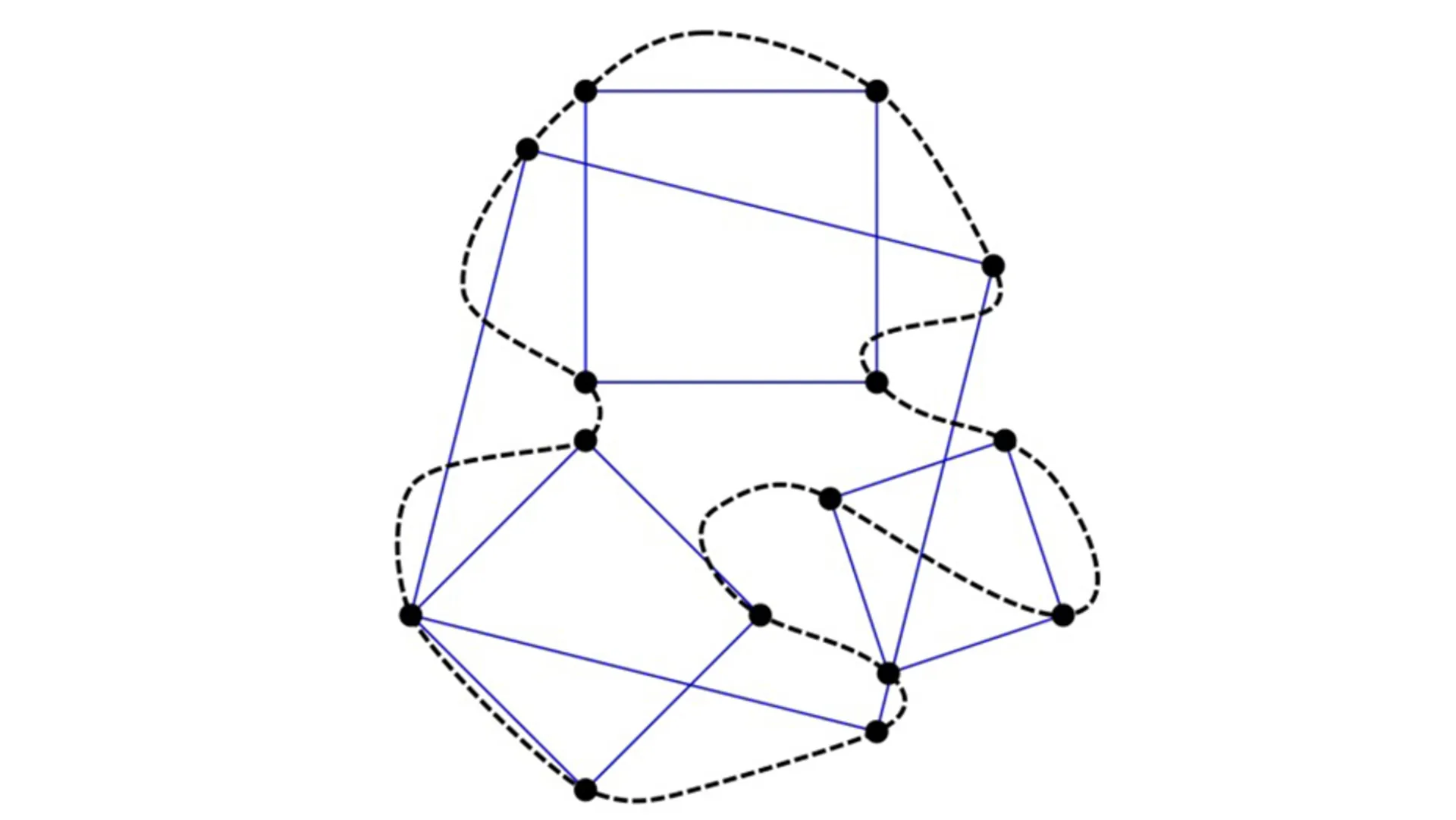
روی کاغذ یک منحنی بسته بکشید. این منحنی میتواند هر تعداد که میخواهید خم و پیچ داشته باشد. تنها شرط این است که باید ابتدای آن را به انتهای آن بچسبانید و نباید خودش را قطع کند. در مرحله بعد سعی کنید چهار نقطه روی منحنی پیدا کنید که بتوان با استفاده از آنها یک مربع رسم کرد. آیا میتوانید این کار را برای هر منحنی انجام دهید؟
این مشکل به مسئله مربع محاط شده (Inscribed Square Problem) مشهور است و میپرسد آیا میتوان در هر منحنی بسته غیرمنقطع، چهار نقطه برای رسم مربع پیدا کرد. این مسئله برای تعدادی دیگر از اشکال هندسی مثل مثلث و مستطیل حل شده است؛ مثلاً ثابت شده که در دایره و مربع میتوان بینهایت مربع محاط شده رسم کرد یا مثلث منفرجه دقیقاً یک مربع محاط دارد؛ اما اینکه برای مربع هم جواب خواهد داد یا خیر، کمی مبهم است و تاکنون اثباتی از سوی ریاضیدانان صورت نگرفته است.
فرضیه پیوستار

ریاضیات مدرن پر از بینهایتها است. از اعداد صحیح مثبت گرفته تا بینهایت خط، مثلث، کُره، مکعب، چندضلعی و غیره. ریاضیات مدرن همچنین ثابت کرده است که قدرهای متفاوتی از بینهایت وجود دارد. اگر بتوان عناصر یک مجموعه را با اعداد صحیح مثبت در یک تناظر یک به یک قرار داد، میگوییم این مجموعه، یک «نامتناهیِ قابلشمارش» است. بنابراین، مجموعه اعداد کامل و مجموعه اعداد گویا یک نامتناهی قابلشمارش هستند.
در قرن نوزدهم، گئورگ کانتور، ریاضیدان آلمانی کشف کرد که مجموعه اعداد حقیقی، غیرقابلشمارش است. این بدان معنا است که اگر سعی کنیم به هر عدد حقیقی یک عدد صحیح مثبت اختصاص دهیم، هرگز قادر به انجام این کار نخواهیم بود؛ حتی اگر از تمام اعداد صحیح استفاده کنیم. درنتیجه، بینهایتهای غیرقابلشمارش را میتوان «بزرگتر» از بینهایتهای قابلشمارش در نظر گرفت.
فرضیه پیوستار (Continuum Hypothesis) در حوزهی یادگیری ماشین و مسائل حلنشدنی در ریاضیات میپرسد که آیا میتوان مجموعهای از اعداد را یافت که نامتناهی باشد و بزرگی آن دقیقاً بین نامتناهی قابلشمارش و غیرقابل شمارش باشد. فرضیه پیوستار نهتنها حل نشده، بلکه ثابت شده که با استفاده از تکنیکهای ریاضی فعلی غیرقابل حل است. این بدان معنا است که هرچند ما حقیقت فرضیه پیوستار را نمیدانیم، این را میدانیم که با روشهای کنونی نمیتوان درستی یا نادرستی آن را اثبات کرد. حل این فرضیه نیازمند چارچوب کاملاً جدیدی است که هنوز ایجاد نشده است.
استراتژی بهینه شطرنج

در نظریه بازی، «استراتژی بهینه» (Optimal Strategy) به مجموعهای محدود از مراحلی گفته میشود که پیروی از آن همواره منجر به پیروزی میشود. ریاضیدانان، استراتژیهای بهینهای برای بازیهایی مانند دوز پیدا کردهاند که اگر از آنها پیروی کنید، همیشه در این بازی برنده خواهید شد.
مدتها است ریاضیدانان بهدنبال استراتژی بهینهای برای بازی شطرنج هستند؛ یعنی مجموعهی معینی از حرکات مهرهها که همیشه پیروزی فرد را در هر شرایطی تضمین کند. مسئلهی استراتژی بهینه شطرنج از این جهت جالب است که با اینکه میدانیم راهحل آن وجود دارد، به احتمال زیاد هرگز نتوانیم آن را پیدا کنیم و این هم بهخاطر پیچیدگی بسیار عظیم بازی شطرنج است.
دلیل این پیچیدگی این است که هر برنامهای که بخواهد شطرنج را حل کند، باید بتواند تمام تغییرات ممکن بازی را برای یافتن حرکت بهینه، پیشبینی و با هم مقایسه کند. این درحالی است که به ازای هر حرکتی که در شطرنج انجام میشود، تعداد بازیهای ممکن بهطور تصاعدی افزایش مییابد. کافی است به جدول زیر نگاهی بیندازید:
تعداد حرکاتها | تعداد بازیهای ممکن |
|---|---|
۱ | ۲۰ |
۲ | ۴۰۰ |
۳ | ۸,۹۰۲ |
۴ | ۱۹۷,۲۸۱ |
۵ | ۴,۸۶۵,۶۰۹ |
۶ | ۱۱۹,۰۶۰,۳۲۴ |
با افزایش تعداد حرکتها، تعداد بازیهای ممکن نیز بهسرعت باورنکردنی افزایش مییابد. بعد از تنها ۵ حرکت، تعداد بازیهای ممکن به بیش از ۶۹ تریلیون میرسد. تخمین زده میشود که تعداد کل موقعیتهای ممکن روی صفحه شطرنج چیزی حدود ۱۰ بهتوان ۱۲۰ باشد (رقمی که به عدد شانون Shannon معروف است.)
این بدان معنا است که اگر قرار بود کامپیوتر تمام موقعیتهای ممکن شطرنج را بررسی کند، حدود ۱۰ به توان ۹۰ سال، یعنی تقریباً ۸٫۳ در ۱۰ بهتوان ۷۹ برابر سن کنونی جهان که ۱۳ میلیارد سال است. با توجه به این محدودیتهای محاسباتی، بعید به نظر میرسد که هرگز بتوانیم شطرنج را دستکم با تکنیکهای فعلی حل کنیم.
درست است که دانشمندان موفق به توسعه هوش مصنوعی شدند که میتواند حتی اساتید بزرگ شطرنج را نیز شکست دهد؛ اما تاکنون هیچ کدام از آنها نمیتوانند خود بازی شطرنج را حل کنند. درعوض، این مدلها در دریایی از ترابایتها داده جستجو میکنند تا استراتژی بردن بازی را پیدا کنند.
مسائل ریاضی حلنشده که آسان بهنظر میرسند
شک نکنید هر مسئله ریاضی که تاکنون حل نشده است، بههیچوجه ساده نیست؛ حل این مسائل یا کلا غیرممکن است یا با تکنیکهای کنونیقابل حل نیست. بااینحال، در دنیای ریاضی مسائلی وجود دارند که ساده به نظر میرسند؛ آنقدر ساده که هرکسی با دانشی ابتدایی از ریاضی میتواند آنها را درک کند؛ اما اثبات این مسائل بهقدری دشوار است که هیچکس موفق به حل آنها نشده است. در ادامه با فهرستی از مسائل بهظاهر ساده ریاضی که البته حلشان مشکل است، آشنا خواهید شد.
حدس اعداد اول دوقلو

اعداد اول، اعدادی هستند که تنها بر خودشان و یک بخشپذیرند. تا آنجاییکه ما میدانیم، تعداد اعداد اول بیشمار است و ریاضیدانان سخت درتلاش برای یافتن بزرگترین عدد اول بعدی هستند.
اما تعدادی از اعداد اول هستند که حاصل تفریق آنها ۲ است، مثل ۴۱ و ۴۳. آیا تعداد این اعداد نیز بینهایت است؟ هرچه اعداد اول بزرگتر میشوند، یافتن این دوقلوها (twin primes) سختتر میشود؛ اما از لحاظ تئوری این اعداد نیز باید بینهایت باشند. مشکل اینجا است که هنوز هیچکسی نتوانسته این بینهایتبودن اعداد اول دوگانه را اثبات کند.
مسئله حرکتدادن مبل
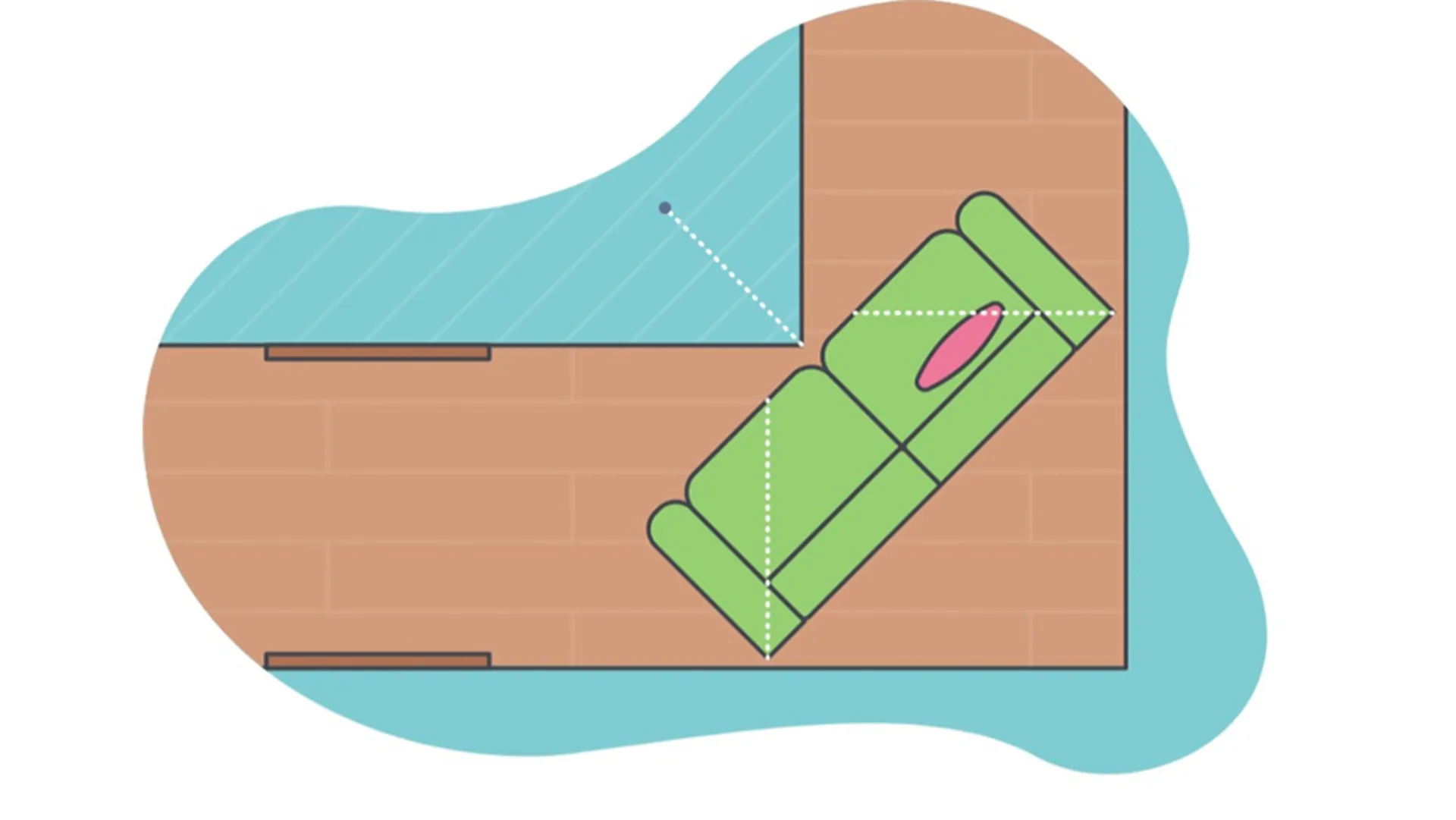
اکثر ما احتمالاً هنگام اثاثکشی به خانه جدید با مشکل جابهجاکردن مبل و حرکتدادن آن از میان راهروهای تنگ و کنج دیوار روبهرو شدهایم. سوالی که برای ریاضیدانان پیش میآید، این است: بزرگترین مبلی که بدون در نظر گرفتن شکل آن میتوانید بدون خم کردنش، از گوشه دیواری با زاویهی ۹۰ درجه عبور دهید، چه ابعادی دارد؟
البته ریاضیدانان این مبل را تنها در بُعد در در نظر میگیرند و کاری به کاربرد آن در دنیای واقعی ندارند. جالب است بدانید بزرگترین حجمی که بتواند در کنج یک زاویه ۹۰ درجه جا شود، «ثابت مبل» (Sofa Constant) نامیده میشود. هیچکس بهطور دقیق نمیداند این عدد چقدر است؛ اما مبلهایی هستند که در این زاویه جا میشوند و مبلهایی هستند که جا نمیشوند. برای همین میدانیم که این ثابت باید چیزی بین ابعاد این دو حالت باشد. درحالحاضر تنها چیزی که دربارهی این مسئله میدانیم این است که ثابت مبل باید چیزی بین ۲٫۲۱۹۵ و ۲٫۸۲۸۴ باشد.
ولی ما مبلهای بزرگی داریم که میدانیم این عدد حداقل بهبزرگی آنها است. ما همچنین مبلهایی داریم که اندازهی آنها با این مقدار سازگار نیست، پس این اندازه از آنها کوچکتر است. درمجموع میدانیم که ثابت مبل چیزی بین ۲.۲۱۹۵ تا ۲.۸۲۸۴ است.
حدس کولاتز

حدس کولاتز (Collatz conjecture) یکی از مشهورترین مسائل حلنشدهی ریاضی است و ازآنجاکه بسیار ساده به نظر میرسد، میتوانید آن را برای کودکان دبستانی توضیح دهید و آنها احتمالاً آنقدر از این مسئله خوششان بیاید که بخواهند جوابی برایش پیدا کنند.
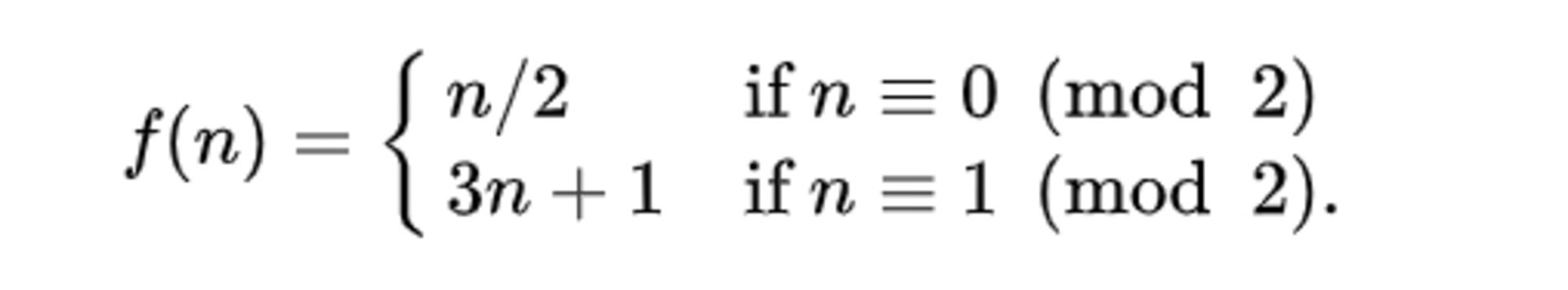
تابع حدس کولاتز
مسئله کولاتز به این صورت است:
ابتدا یک عدد بهدلخواه انتخاب کنید. اگر این عدد زوج بود، آن را به ۲ تقسیم کنید و اگر فرد بود آن را در ۳ ضرب و سپس با ۱ جمع کنید. این مراحل را برای عدد جدید بهدستآمده ادامه دهید. عددی که سرانجام به آن میرسید، همیشه ۱ خواهد بود. بهعنوان مثال اگر عدد انتخابی ۶ باشد، انجام این مراحل، این اعداد را نشان خواهد داد: ۶، ۳، ۱۰، ۵، ۱۶، ۸، ۴، ۲، ۱.
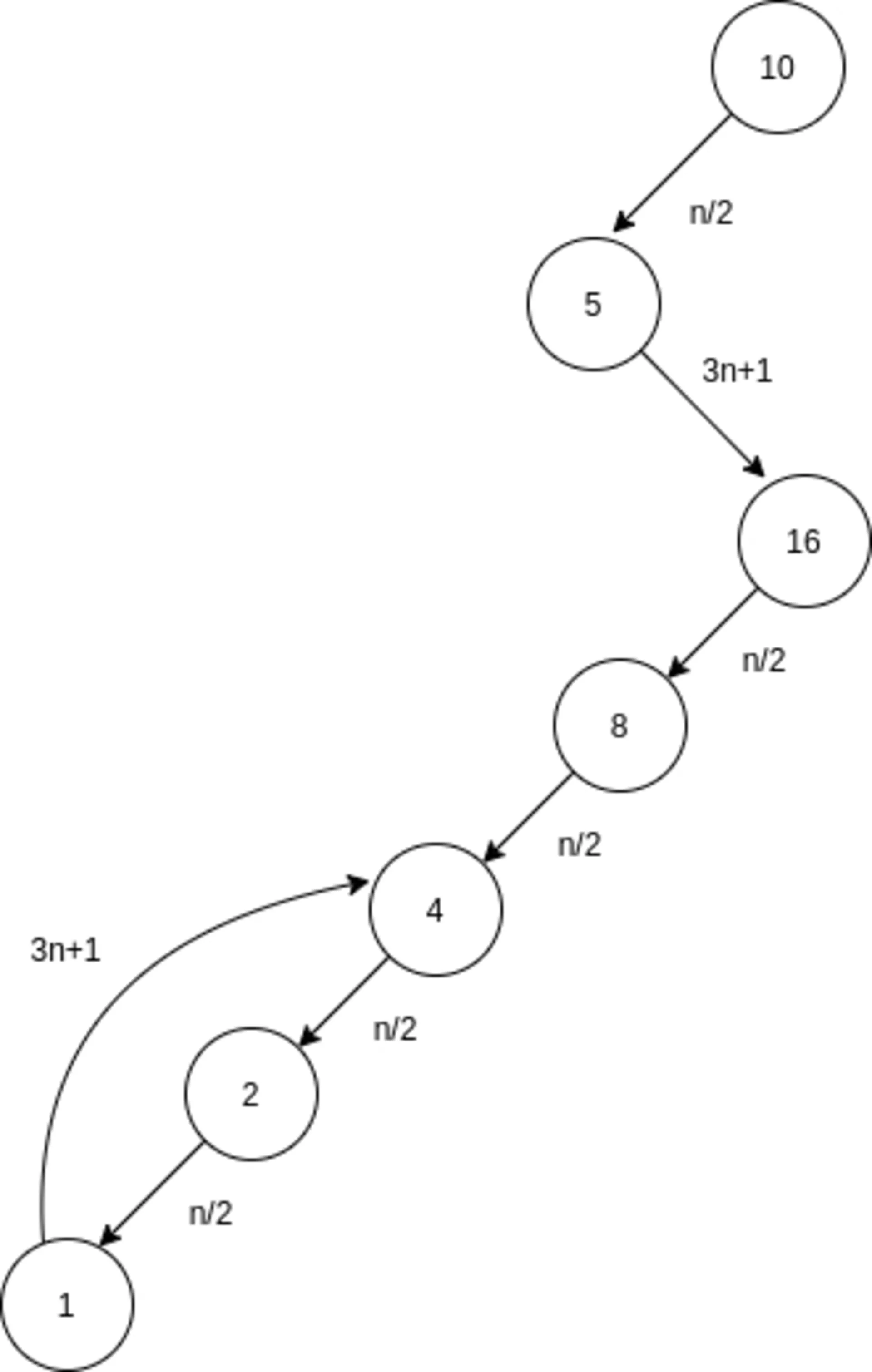
ریاضیدانان میلیونها عدد پیدا کردهاند که از این قاعده پیروی میکند؛ اما مشکل اینجا است که هنوز نتوانستهاند عددی پیدا کنند که طبق این قاعده پیش نرود. احتمال دارد که عددی بسیار بزرگ که میل به بینهایت دارد یا عددی که در یک چرخه گیر کند، هرگز به یک نرسد؛ ولی تابهحال کسی نتوانسته این عدد را پیدا کند.
حدس بیل
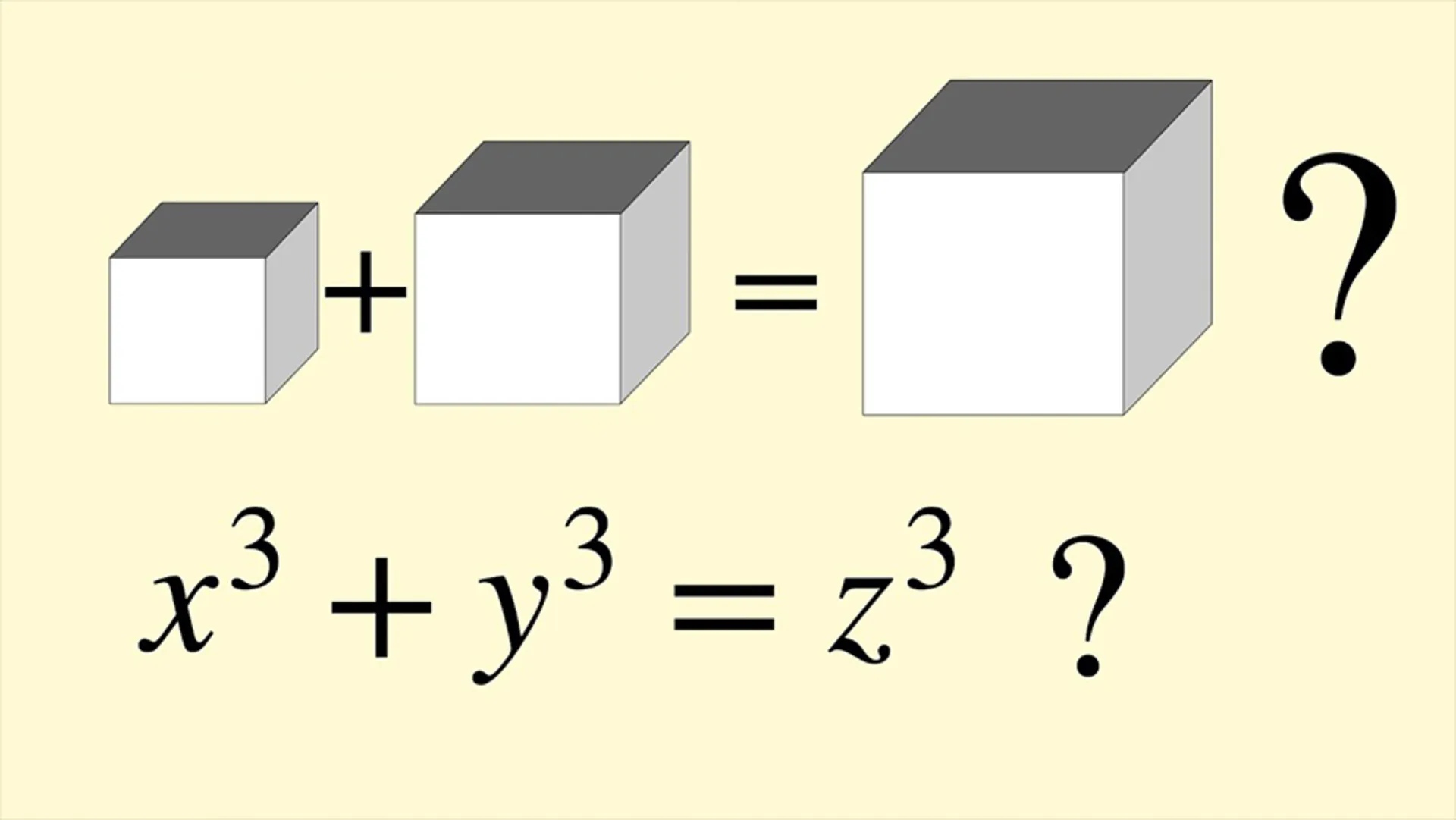
حدس بیل (Beal Conjecture) یکی دیگر از مسائل مهم ریاضی است که به نظر ساده میآید؛ اما هنوز کسی موفق به حل آن نشده است.
براساس این مسئله، اگر Ax + By = Cz و A ،B ،C، اx، اy و z همگی اعداد صحیح مثبت باشند ( اعداد بزرگتر از صفر)، A ،B و C باید همگی یک عامل اول مشترک داشته باشند. عامل اول مشترک بدین معنا است که هر یک از این اعداد باید بر عدد اول یکسانی پخشپذیر باشد. مثلاً عامل اول مشترک اعداد ۱۵، ۱۰ و ۵ برابر است با ۵ و همه آنها بر عدد اول ۵ بخشپذیرند.
این مسئله تا اینجا ساده به نظر میرسد و شاید نمونه آن را در درس جبر دبیرستان حل کرده باشید. اما مشکل اینجا است که ریاضیدانان هنوز نتوانستهاند حدس بیل را با x، y و z بزرگتر از ۲ حل کنند. بهعنوان مثال اگر عامل اول مشترک ما ۵ باشد، آنوقت ۵۱ + ۱۰۱ = ۱۵۱ اما ۵۲ + ۱۰۲ ≠ ۱۵۲.
این مسئله را میلیاردر اهل تگزاس بهنام اندرو بیل مطرح کرده و به کسی که سرانجام موفق به حل آن شود، یک میلیون دلار جایزه از سمت انجمن ریاضی آمریکا اهدا خواهد شد.
حدس گلدباخ
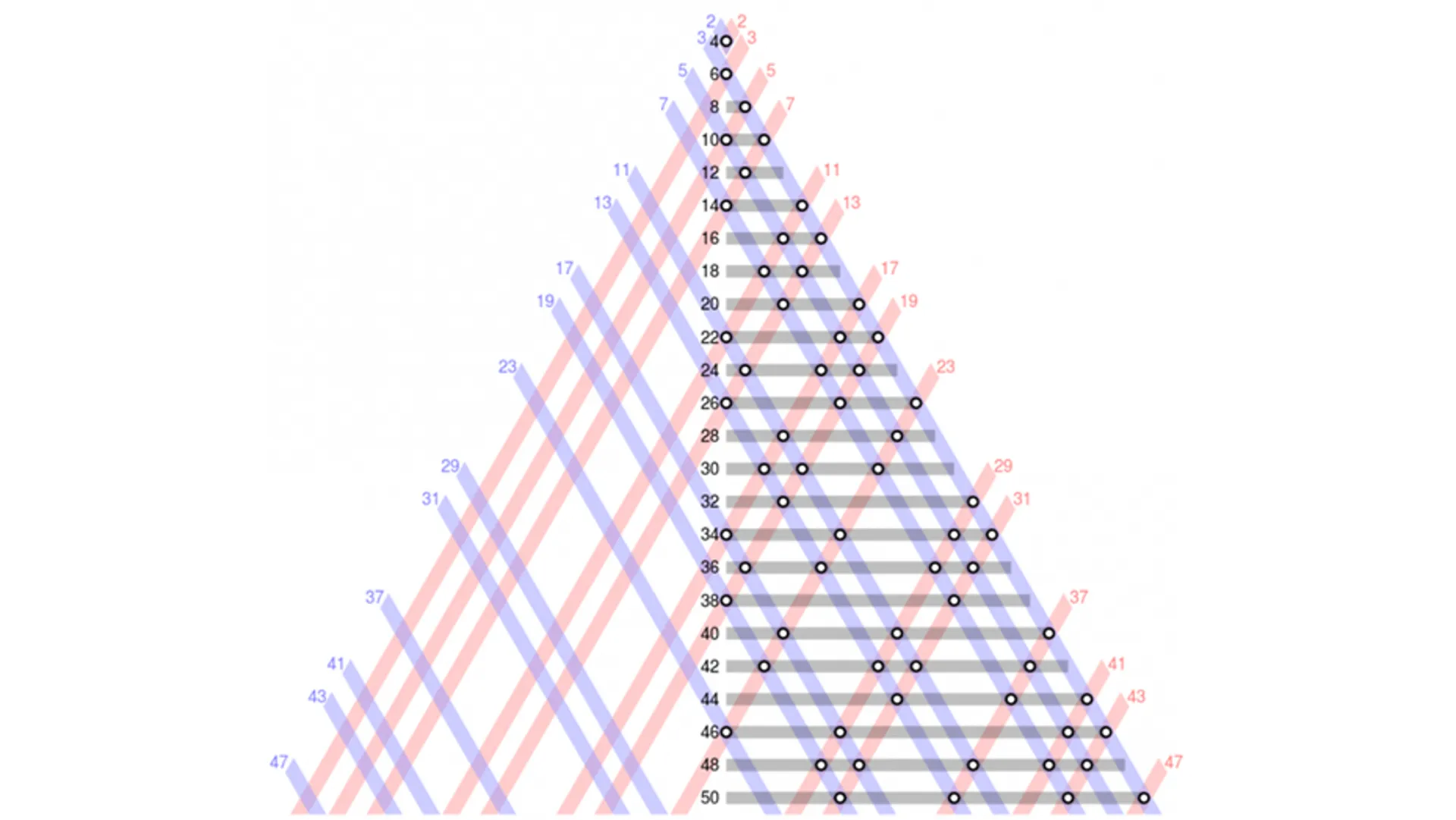
حدس گلدباخ (Goldbach's conjecture) نیز مانند حدس اعداد اول دوقلو، مسئله حلنشده دیگری دربارهی اعداد اول است که بهظاهر ساده اما حل آن بهشدت دشوار است. این مسئله میگوید آیا هر عدد صحیح زوج بزرگتر از ۲، مجموع دو عدد اول است؟ شاید بگویید واضح است که پاسخ مثبت است؛ چراکه عدد ۴ مجموع دو عدد اول ۳ و ۱ یا عدد ۶ مجموع دو عدد اول ۵ و ۱ است و این روند بههمینصورت ادامه دارد.
راستش را بخواهید، این مسئله از نظر کریستین گلدباخ، ریاضیدان آلمانی، که آن را در سال ۱۷۴۲ مطرح کرد، به همین شکل حل شده بود. او با اطمینان کامل گفته بود «هر عدد صحیح زوج بزرگتر از ۴ میتواند بهصورت مجموع دو عدد اول نوشته شود.»
اما با وجود قرنها تلاش، تابهحال هیچکس نتوانسته است ثابت کند که این قاعده همیشه و برای تمام اعداد جواب میدهد. حقیقت این است که اگر ما اعداد را بزرگ و بزرگتر کنیم و بههمین روند ادامه دهیم، شاید به عددی برسیم که برابربا مجموع دو عدد اول نباشد یا به عددی برسیم که تمامی قوانین و منطقی را که تابهحال از آن استفاده میکردیم، نقض کند. بیشک ریاضیدانان تا جوابی برای این مسئله پیدا نکنند، دست از تلاش برنخواهند داشت.
تا به امروز، حدس گلدباخ برای همه اعداد صحیح زوج تا ۴ در ۱۰۱۸ تأیید شده است؛ اما اثبات تحلیلی آن هنوز از دسترس ریاضیدانان دور است. بااینحال، اجماع عمومی بر این است که این حدس بهخاطر ماهیت توزیع اعداد اول درست است. چراکه هرچه یک عدد صحیح بزرگتر باشد، احتمال بیشتری وجود دارد که بتوان آن را به صورت مجموع دو عدد دیگر بیان کرد. بنابراین، هرچه یک عدد صحیح بزرگتر باشد، احتمال اینکه حداقل یکی از این ترکیبها فقط از اعداد اول تشکیل شده باشد، بیشتر است.
مسائل ریاضی حل نشده جایزهدار (مسائل جایزه هزاره)
مسائل جایزه هزاره (Millennium Problems) هفت مسئله ریاضی هستند که توسط انجمن ریاضی کلی (Clay Mathematics Institute) در سال ۲۰۰۰ و برای جشن گرفتن هزاره جدید مطرح شدهاند. هر کسی که بتواند یکی از این مسائل را حل کند، برندهی یک میلیون دلار جایزه نقدی خواهد شد و حلکردن این مسائل تأثیرات بزرگی بر حوزهی مربوط یا حتی فراتر از آن خواهد داشت.
این هفت مسئله عبارتاند از:
- P دربرابر NP
- حدس هاج
- فرضیه ریمان
- نظریه یانگ-میلز
- معادلات ناویر-استوکس
- حدس برچ و سوینرتون-دایر
- حدس پوانکاره
از میان این هفت مسئله، حدس پوانکاره در سال ۲۰۰۳ توسط گریگوری پرلمان (Grigori Perelman)، ریاضیدان روسی، حل شد؛ هرچند او از قبول جایزه انجمن کلی و البته تمام جوایز و مدالهای دیگر برای دستاوردهایش خودداری کرد.
بیش از دو دهه از زمان مطرحشدن مسائل جایزه هزاره میگذرد و شش مسئلهی دیگر کماکان حلنشده باقی ماندهاند. در ادامه به توضیح این مسائل خواهیم پرداخت؛ شاید شما بتوانید آنها را حل کنید!
فرضیه ریمان
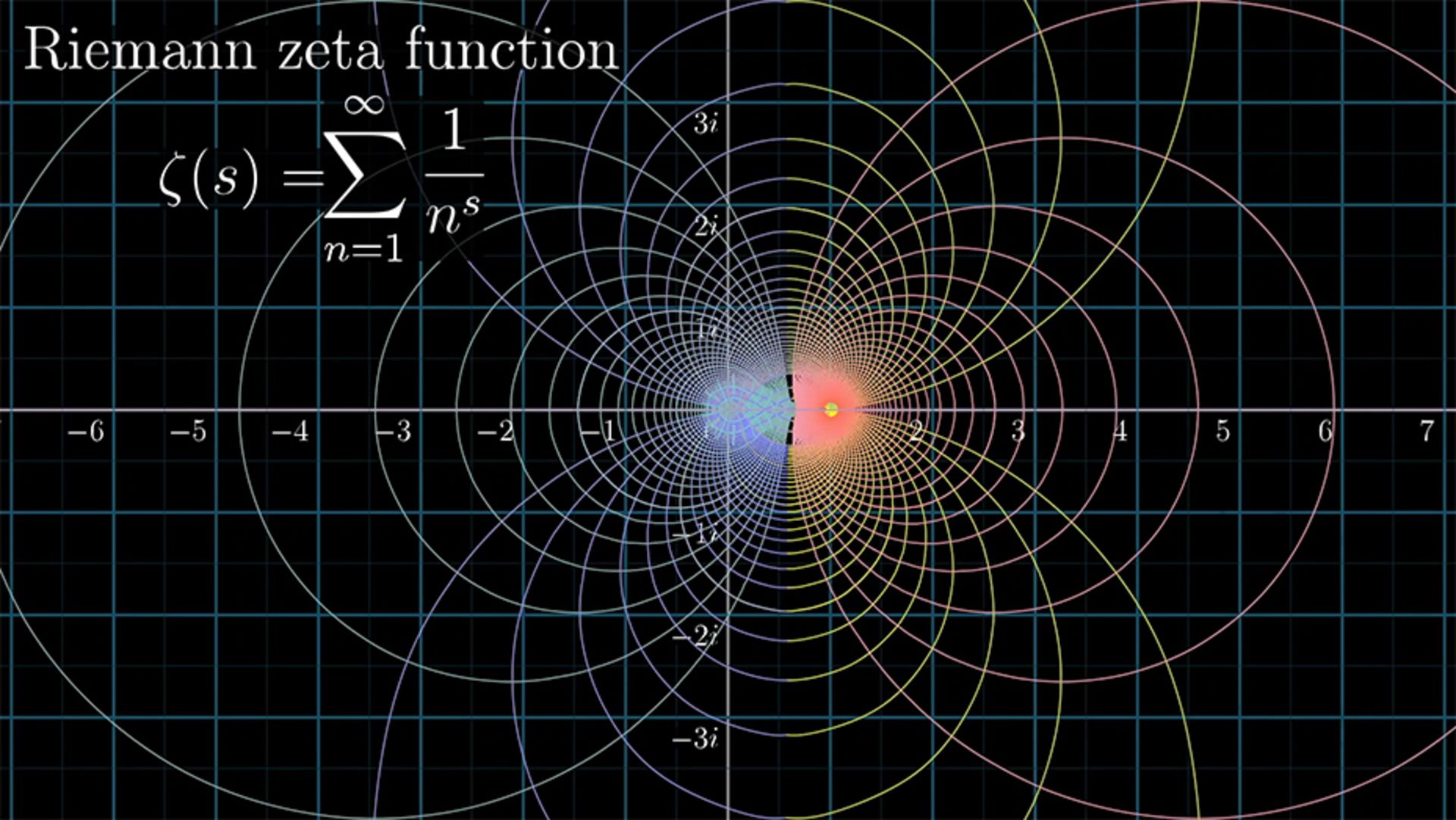
مهمترین مسئلهی حل نشده در ریاضیات محض به فرضیه ریمان (Riemann Hypothesis) مشهور است. این مسئله را برنهارت ریمان، ریاضیدان آلمانی قرن نوزدهم مطرح کرده است که آثارش در زمینه آنالیز و هندسه دیفرانسیل، پایه ریاضی نظریهی نسبیت عام شد.
فرضیه ریمان از سال ۱۸۵۹ تاکنون حل نشده باقی مانده و بهقدری دشوار است که دیوید هیلبرت، از تأثیرگذارترین ریاضیدانان در پیدایش و گسترش مکانیک کوانتومی و نظریه نسبیت، دربارهی آن گفت:
اگر قرار بود بعد از هزار سال از خواب بیدار شوم، اولین سوالی که میپرسیدم این بود: آیا فرضیه ریمان اثبات شده است؟
جالب است بدانید هیلبرت در سال ۱۹۰۰، بیست و سه سؤال ریاضی که تا آن زمان حل نشده بودند را مطرح کرده بود که فرضیه ریمان یکی از آنها بود. برخی از این سؤالها که به مسائل هیلبرت شهرت دارند، حل شدهاند و تأثیر بسزایی بر ریاضیات قرن بیستم گذاشتند.
فرضیه ریمان درواقع از شما میخواهد اثبات کنید تابع زتا ریمان در چه شرایطی برابر با صفر است. بهعبارت دیگر:
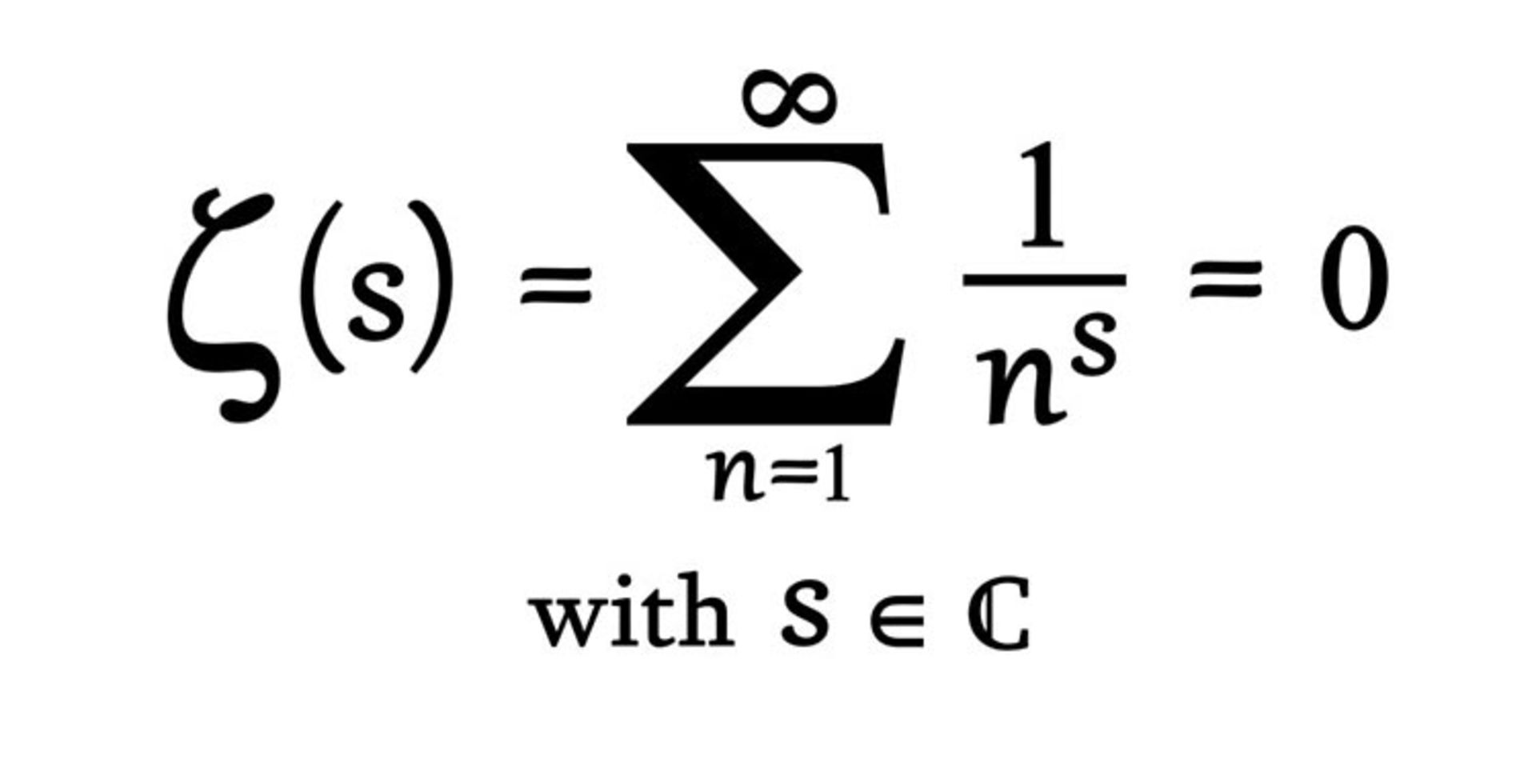
این تابع در ظاهر، ساده به نظر میرسد؛ اما پیچیدگی آن روی نمودار ظاهر میشود. برای مثال، به نمودار |ζ(1/2+iy)| (محور عمودی) بهعنوان تابعی از y (محور افقی) نگاه کنید.
همانطورکه میبینید، تابع زتا برای مقادیر ۱۴، ۲۱، ۲۵ و الیآخر روی محور افقی، به صفر نزدیک میشود. به اینها صفرهای تابع زتا میگویند و از اهمیت بسیاری برخوردارند، چراکه رفتارشان هیجانانگیز است. فرضیه ریمان هم درواقع گزارهای دربارهی نحوه توزیع این صفرها است. ریمان میگوید تابع زتا تنها زمانی به صفر میرسد که با اعداد صحیح زوج منفی و اعداد مختلط با قسمت واقعی ۱/۲ سروکار داشته باشیم. مشکل اینجا است که اگرچه بیش از ۲۵۰ میلیون صفر این فرضیه را اثبات کردهاند، هنوز ثابت نشده که این موضوع برای تمام صفرها صدق میکند.

توزیع اعداد اول (خطوط زرد) در مجموعه اعداد طبیعی از ۰ تا ۱۰۰۰
فرضیه ریمان از این جهت بسیار مهم است که اعداد اول (که فقط بر یک و خودشان تقسیمپذیرند) اساسیترین و اسرارآمیزترین مفهوم در ریاضیات هستند. وقتی اعداد اول را به صورت مجموعه خطی پشت سر هم مینویسیم، هیچ الگویی در نحوه توزیع آنها ظاهر نمیشود و بههمین خاطر نمیتوانیم تمام اعداد اول را پیشبینی کنیم. اما وقتی این اعداد را به کمک تابع زتا ریمان روی نمودار میآوریم، الگوی جالبی از صفرهای ریمان روی آن ظاهر میشود که اگر بتوانیم آن را برای تمام اعداد ثابت میکنیم، آنوقت میتوانیم بگوییم الگوی پنهان توزیع اعداد اول را سرانجام کشف کردهایم. بدینترتیب میتوانیم با دقت بسیار بالا تعداد اعداد اول در هر بازه معینی را تعیین کنیم.
شاید بپرسید داشتن تابعی برای تعریف اعداد اول اصلاً چه اهمیتی دارد؟ بسیاری از ریاضیدانان اعداد اول را بهعنوان اتمهای تشکیلدهندهی تمام اعداد دیگر میبینند، زیرا میتوانید با استفاده از اعداد اول به هر عددی برسید. در فرضیه ریمان، دامنهای که روی خط عددی از مقادیری ایجاد میشود که تابع زتا را صفر میکند، همانند فواصل بین سطوح انرژی در سیستمهای کوانتومی است و این یعنی نوعی رابطه بین اجزای سازنده اعداد با اعداد اول و اجزای سازنده ماده با اتم وجود دارد و حل این فرضیه ما را به درک جدیدی از ماده خواهد رساند.
مسئله P درمقابل NP

P درمقابل NP مسئله حل نشده مهمی در علوم کامپیوتر است و میپرسد آیا هر مسئلهای که صحت جوابهای آن را بتوان بهسرعت ارزیابی کرد (NP)، بهسرعت هم قابل حلشدن است (P)؟ این مسئله را استیون کوک، دانشمند کامپیوتر در سال ۱۹۷۱ مطرح کرد.
بیایید برای فهم بهتر این مسئله یک مثال بزنیم. اگر به شما عددی را بدهند و بگویند این عدد از حاصلضرب کدام دو عدد اول بدست آمده است، آیا میتوانید به پاسخ درستی برسید؟ اگر این عدد کوچک باشد، جواب ساده است. مثلاً ۱۵ از ضرب دو عدد ۵ و ۳ حاصل میشود. اما اگر عدد موردنظر ما ۲۰۰ رقم داشته باشد، سالها زمان لازم است تا دو مضرب آن پیدا شود.
حالا این سؤال را برعکس کنیم؛ اگر به شما دو عدد اول را دهند و بگویند آیا از حاصلضرب این دو، عدد x حاصل میشود، پیداکردن جواب این سؤال بهراحتی انجام عملیات ضرب است. بهعبارت دیگر، شما با ضرب این دو عدد میتوانید بهسرعت صحت جواب را ارزیابی کنید. اما همانطور که دیدید، برعکس این قضیه آنقدر زمان میبرد که حل آن تقریباً ناممکن است.
در حوزه علوم کامپیوتر، مسئلهای که جوابش بهسرعت تعیین میشود، P و مسئلهای که صرفاً صحت جوابهای آن بهسرعت تأیید میشود، NP نام دارد. درواقع، اینکه مسائل بتوانند بهسرعت حل شوند، یا به زبان علوم کامپیوتر، زمان اجرای الگوریتم آنها «چندجملهای» (Polynomial Time) باشد، از اهمیت بسیاری برخوردار است؛ چراکه اگر حل مسئلهای بخواهد صدها یا هزاران سال طول بکشد، حل آن عملا ناممکن است.
مسئله استیون کوک دقیقاً این را میپرسد:
آیا میتوانیم در ازای هر الگوریتم NP که زمان اجرای آن چند جملهای است، الگوریتمی با زمان اجرای چند جملهای برای P داشته باشیم؟
روزی که کسی بتواند سرانجام ثابت کند P=NP، بسیاری از ریاضیدانان از کار بیکار میشوند. چراکه P=NP به این معنی است که اثبات یک نظریه ریاضی با ارزیابی صحت جوابهای آن یکی است. حتی بدتر از آن، تمام سیستمهای بانکی نیز از کار میافتند؛ چراکه رمزگشایی از کلماتعبور که با مضرب بسیار بزرگی از اعداد اول رمزنگاری میشوند، در کسری از ثانیه ممکن میشود. برای آشنایی بیشتر با این موضوع پیشنهاد میکنم مقاله الگوریتم شور به زبان ساده؛ رمزگشایی داده در کامپیوتر کوانتومی را مطالعه کنید.
حدس هاج

حدس هاج (Hodge Conjecture) یکی از مسائل مهم حل نشده در هندسه جبری و هندسه مختلط است که چگونگی تشکیل ساختارهای پیچیدهی ریاضی از اجزای ساده را بررسی میکند و درواقع میکوشد این دو مفهوم مختلف ریاضی را به هم پیوند دهد.
در قرن بیستم، ریاضیدانان روش مهمی برای مشاهده و بررسی اجسام پیچیده کشف کردند؛ بهاین صورت که اجسامی را که بهطور فزایندهای بزرگتر میشدند، کنار هم قرار میدهند تا به نزدیکترین شکل به جسم اصلی برسند. این تکنیک بهقدری مفید بود که در بسیاری از حوزههای دیگر نیز به کار گرفته شد و درنهایت، اجسام پیچیدهای که ریاضیدانان به این روش دستهبندی کردند، در اختراعات شگفتانگیزی به کار رفتند.
متأسفانه، ازطریق این تعمیمها، خاستگاه هندسی این فرایند از بین رفت و تلاش بر این بود که این اجزا بدون فرمول و پشتوانه هندسی به هم پیوند داده شوند. حالا حدس هاج میپرسد آیا برای این مفهوم، رابط هندسی وجود دارد؟
نظریه یانگ-میلز

نظریه یانگ-میلز (Yang-Mills Theory) یکی دیگر از مسائل حل نشده جایزهدار است که به حوزهی فیزیک کوانتوم مربوط میشود. این نظریه، ذرات را با استفاده از تقارن ریاضی تعریف میکند.
در طول شش دههی گذشته، تئوری یانگ-میلز به سنگ بنای فیزیک نظری تبدیل شده است؛ چراکه به نظر میرسد تنها نظریه نسبیت کوانتوم چندجسمی کاملاً سازگار با چهار بعد فضازمان باشد و بههمین خاطر، پایه مدل استاندارد فیزیک ذرات است که ثابت شده نظریه درستی برای انرژیهایی است که میتوانیم اندازهگیری کنیم.
نظریه یانگ-میلز درواقع تعمیم نظریه یکپارچه الکترومغناطیس یا همان «معادلات ماکسول» است که توسط جیمز کلرک ماکسول، فیزیکدان اسکاتلندی مطرح شد و برای توصیف نیروی ضعیف و نیروی قوی ذرات زیراتمی بر حسب ساختار هندسی یا میدان کوانتومی به کار میرود.
این نظریه در سال ۱۹۵۴ توسط دو فیزیکدان به نامهای چن نینگ یانگ و رابرت ال. میلز ارائه شد و بر خاصیت مکانیک کوانتومی موسوم به «شکاف جرم» (Mass Gap) تکیه دارد که درواقع تفاوت انرژی بین پایینترین سطح (خلا) با کمترین سطح بعدی و معادل جرم سبکترین ذره است. دانشمندان معتقدند شکاف جرمی عاملی است که باعث شده نیروی قوی تنها در فواصل بسیار کوچک، یعنی درون هستههای اتمی، وجود داشته باشد.
نظریه یانگمیلز یکپارچگی نیروی الکترومغناطیسی و نیروی ضعیف را توصیف میکند؛ نیروی اول باعث میشود الکترونها به دور پروتون بچرخند و نیروی دوم باعث میشود یک نوترون به یک الکترون و یک پروتون تجزیه شود. تفاوت این دو نیرو مانند تفاوت بین قمری است که در حین چرخش به دور سیاره دور خود میچرخد و قمری که در حین چرخش به دور سیاره، بهدور خود نمیچرخد. نیرویی که قمر را در مدار سیاره نگه میدارد، صرفنظر از اینکه به دور خود میچرخد یا خیر، یکسان است. منظور از یکپارچگی همین است؛ اینکه نشان دهیم پشت این دو چیز متفاوت، نیروی یکسانی وجود دارد.
معادلات ناویه–استوکس
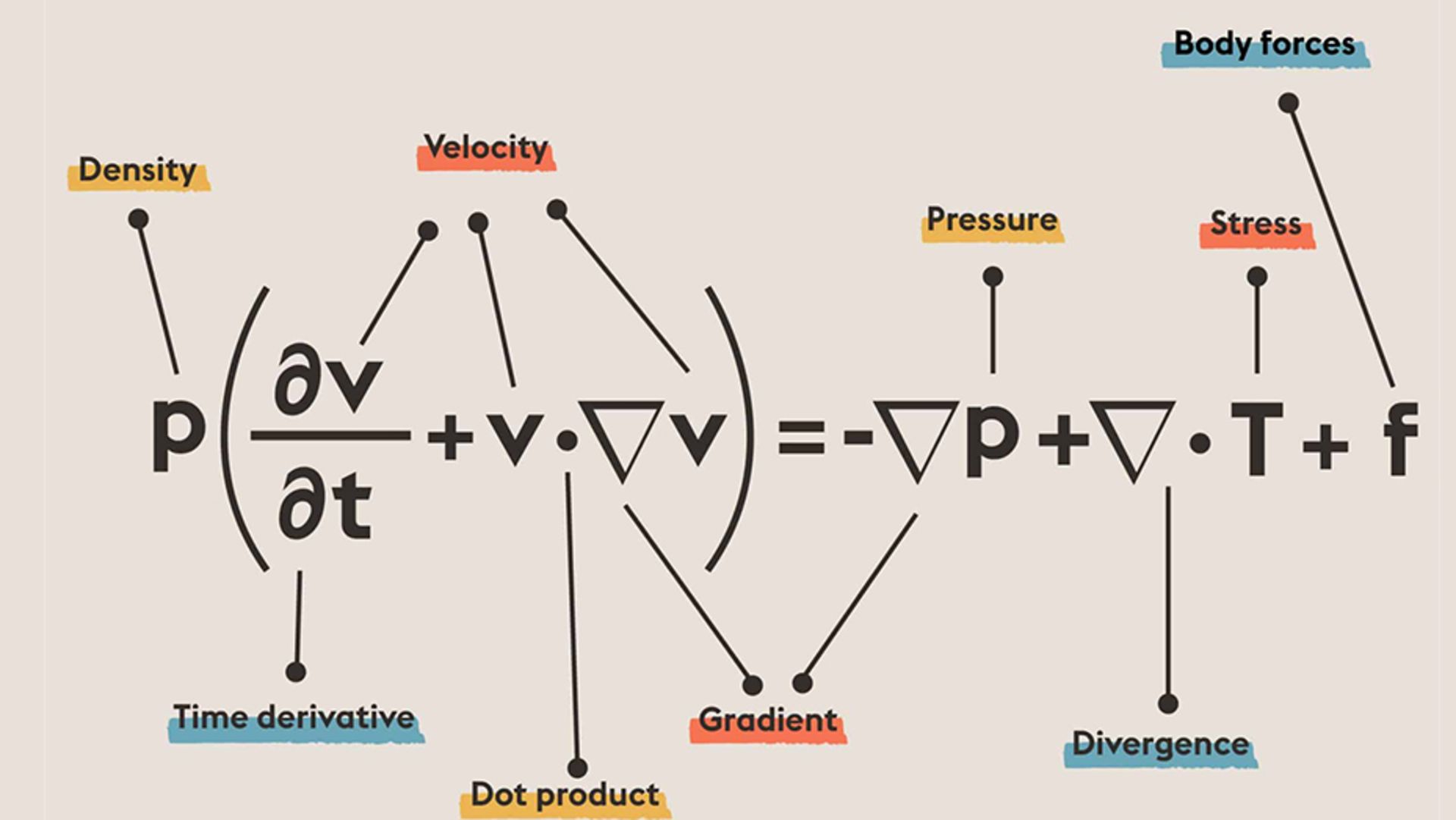
معادلات ناویه-استوکس (Navier Stokes Equations) یکی دیگر از مسائل جایزه هزاره است که به مجموعهای از معادلات دیفرانسیل مربوط میشود که حرکت سیالات تراکمپذیر را توصیف میکند. بهطور خلاصه، معادلات ناویه-استوکس رفتار سیالات را توصیف میکند.
این معادله با اعمال قانون دوم نیوتن در مورد سیالات به دست میآید و پرواز هواپیماها، تولید برق، پیشبینی آبوهوا و حتی ساخت قایق و کشتی نیز به آن وابسته است. حتی کمپانی انیمیشنسازی پیکسار نیز از معادلات ناویه-استوکس برای پویانمایی آثار خود استفاده میکند.
این معادلات اگرچه ساده به نظر میٰسند، در حالت سهبعدی بهسرعت پیچیده میشوند. چارلز ففرمن، استاد دانشگاه پرینستون میگوید: «میتوان حل معادلات ناویر-استوکس را نسبتاً بهسادگی و با اعتماد به نفس بالا شروع کنید؛ اما راهحلها ممکن است بهطور باورنکردنیای غیرقابل پیشبینی باشند».
گفته میشود اگر ریاضیدانان بتوانند پدیده ناویه-استوکس را از این حالت غیرقابل پیشبینی بیرون آورند، تغییرات شگرفی در زمینه دینامیک سیالات حاصل خواهد شد. به گفتهی ففرمن، اگر این معادلات به اثبات برسد، «دستاوردی فوقالعاده در بالاترین حد خواهد بود.»
حدس برش و سوینرتون-دایر
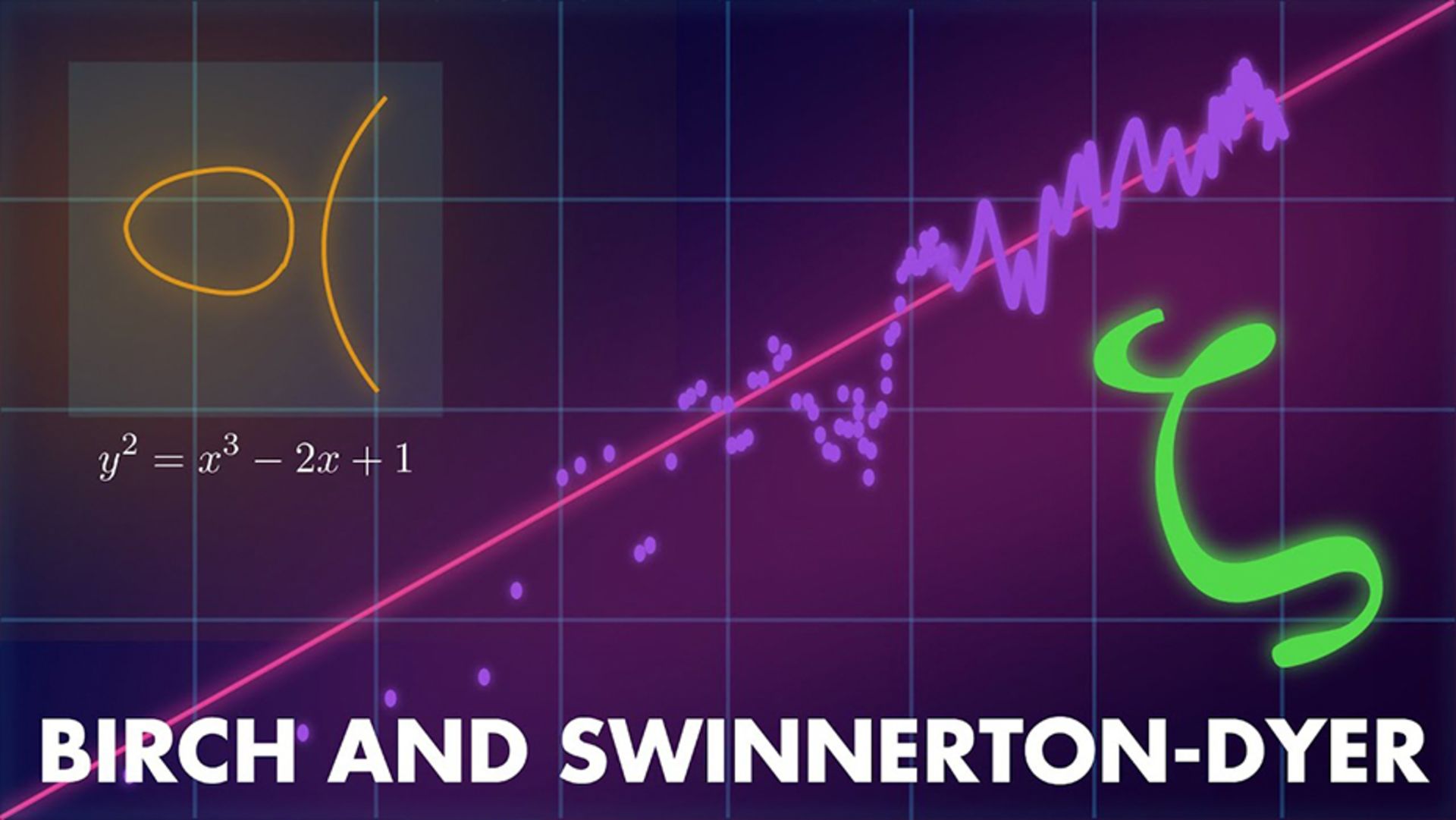
اوایل دهه ۱۹۶۰ در انگلستان، ریاضیدانان بریتانیایی برایان برش و پیتر سوینرتون-دایر از کامپیوتر EDSAC که جزو اولین کامپیوترهای ساخت انگلیس بود، برای انجام تحقیقات عددی منحنیهای بیضوی استفاده کردند. آنها براساس این نتایج عددی، حدس برش و سوینرتون-دایر (Birch and Swinnerton-Dyer conjecture) را مطرح کردند که آخرین مسئله حلنشده یک میلیون دلاری در این فهرست است.
حدس برش و سوینرتون-دایر میگوید یک منحنی بیضوی درصورتی که تابع مربوط به آن برابر با صفر باشد، دارای تعداد نامتناهی نقطه گویا (راهحل) است و درصورتیکه تابع صفر نباشد، دارای تعداد محدودی از نقاط گویا است. بهعبارت دیگر، این مسئله میخواهد ثابت کنید اگر یک منحنی بیضی بینهایت راهحل داشته باشد، در نقاط خاصی از سری L برابر با صفر خواهد بود.
این نظریه بهطور گسترده در رمزنگاری استفاده میشود و برای حل بسیاری از مسائل از جمله قضیه آخر فِرما (Fermat’s final theorem) اهمیت زیادی دارد.
جمعبندی
تمام مسائلی که در این مطلب به آنها اشاره شد، بهویژه مسائل جایزه هزاره، برای افراد معمولی مطرح نشدهاند و حتی توضیح و فهم آنها نیز دشوار است، چه برسد به حلشان. ریاضیدانان با تمرکز روی این مسائل درواقع تلاش میکنند مسیری به سمت آینده باز کنند و چهبسا راهحل بسیاری از آنها نیازمند تکنیکهایی باشد که بشر قرنها بعد به آنها دست پیدا کند. بههمین خاطر حل این مسائل زماندار نیست و هر زمانی که دانشمندی بتواند حتی یکی از این مسائل دشوار را حل کند، پیشرفتهای علمی سرعت بیشتری به خود میگیرند. این مسائل ریاضی درحقیقت به شکلگیری نظریههای جدید منجر خواهند شد و ارزش آنها نیز در همین نهفته است.
در دنیای ریاضیات، بهویژه در حوزهی نظریه اعداد که طرح مسئله آسان؛ اما حل آن دشور است، شکیبایی از همه چیز مهمتر است. ریاضیدانان میگویند باید به این مسائل به مدت طولانی فکر کرد و برایشان اهمیت قائل بود. پیشرفت کمکم حاصل میشود و اگر همین طور به کندن ادامه دهیم، سرانجام به الماس میٰرسیم.
سؤالات متداول
مهمترین مسئله ریاضی حل نشده کدام است؟
مهمترین مسئلهی حل نشده در ریاضیات محض به فرضیه ریمان (Riemann Hypothesis) مشهور است. این مسئله را برنهارت ریمان، ریاضیدان آلمانی قرن نوزدهم مطرح کرده و میخواهد اثبات کنید تابع زتا ریمان در چه شرایطی برابر با صفر است. این مسئله میکوشد برای توزیع اعداد اول که اساسیترین و اسرارآمیزترین مفهوم در ریاضیات هستند، الگوی مشخصی پیدا کند.
مسائل جایزه هزاره کدامند؟
مسائل جایزه هزاره (Millennium Problems) هفت مسئله ریاضی هستند که حل هر یک از آنها جایزه یک میلیون دلاری به همراه دارد. این هفت مسئله عبارتاند از: P دربرابر NP، حدس هاج، فرضیه ریمان، نظریه یانگ-میلز، معادلات ناویر-استوکس، حدس برچ و سوینرتون-دایر و حدس پوانکاره که مورد آخری در سال ۲۰۰۳ توسط گریگوری پرلمان، ریاضیدان روسی، حل شد.
مسئله P درمقابل NP چیست؟
P درمقابل NP مسئله حل نشده مهمی در علوم کامپیوتر و از مسائل جایزه هزاره است و میپرسد آیا هر مسئلهای که صحت جوابهای آن را بتوان بهسرعت ارزیابی کرد (NP)، بهسرعت هم قابل حلشدن است (P)؟ روزی که کسی بتواند سرانجام ثابت کند P=NP، بسیاری از ریاضیدانان از کار بیکار میشوند. چراکه P=NP به این معنی است که اثبات یک نظریه ریاضی با ارزیابی صحت جوابهای آن یکی است.
نظرات